题目内容
7.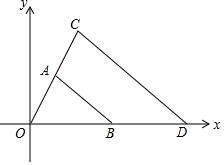 如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )
如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )| A. | (2,3) | B. | (2,4) | C. | (3,3) | D. | (3,4) |
分析 利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,-ky),进而求出即可.
解答 解:∵△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点A与点C是对应点,
∴点C的坐标为(1×2,2×2),即(2,4),
故选:B.
点评 本题考查的是位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
相关题目
17.近似数-0.03750的有效数字有( )个.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
15.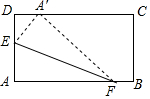 如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
 如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )| A. | $\frac{5}{3}$ | B. | $\frac{8}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{5}$ |
12.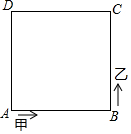 如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )
如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )
 如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )
如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )| A. | AB边 | B. | BC边 | C. | CD边 | D. | AD边 |
19.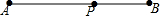 已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )
已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )
①AP2=AB•PB;②$AP=\frac{{\sqrt{5}-1}}{2}AB$;③$PB=\frac{{3-\sqrt{5}}}{2}AB$;④$\frac{AB}{AP}$=$\frac{\sqrt{5}+1}{2}$;⑤$\frac{AP}{PB}$=$\frac{\sqrt{5}+1}{2}$.
 已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )
已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )①AP2=AB•PB;②$AP=\frac{{\sqrt{5}-1}}{2}AB$;③$PB=\frac{{3-\sqrt{5}}}{2}AB$;④$\frac{AB}{AP}$=$\frac{\sqrt{5}+1}{2}$;⑤$\frac{AP}{PB}$=$\frac{\sqrt{5}+1}{2}$.
| A. | ①②④ | B. | ②③④ | ||
| C. | ①②不是,其余都是 | D. | 以上任何一种均可 |
11.某服装店老板以60元出售一件衣服,结果获利25%,问这件衣服的进价是( )
| A. | 40 | B. | 48 | C. | 50 | D. | 80 |
 如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20.
如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20.