题目内容
10.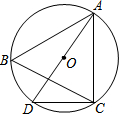 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
分析 由圆周角定理可知∠ACD=90°,∠B=∠D,由勾股定理求出CD=$\frac{1}{2}$AD,得出∠DAC=30°,求出∠D=60°,再由圆周角定理即可得出结果.
解答 解:∵AD是⊙O的直径,
∴∠ACD=90°.
Rt△ACD中,AD=2r=10,AC=5$\sqrt{3}$.
根据勾股定理,得:CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=5,
∴CD=$\frac{1}{2}$AD,
∴∠DAC=30°,
∴∠B=∠D=90°-30°=60°;
故选:D.
点评 此题主要考查的是圆周角定理、勾股定理;能够根据圆周角定理将所求角转化到直角三角形中,是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.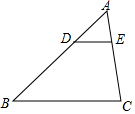 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{DB}$ | D. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ |
5.解方程$3x+\frac{2x-1}{3}=3-\frac{x+1}{2}$时,去分母正确的是( )
| A. | 18x+2(2x-1)=18-3(x+1) | B. | 3x+2(2x-1)=3-3(x+1) | ||
| C. | 9x+(2x-1)=6-(x+1) | D. | 3x+(2x-1)=3-(x+1) |
15.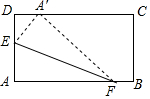 如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
 如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )| A. | $\frac{5}{3}$ | B. | $\frac{8}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{5}$ |
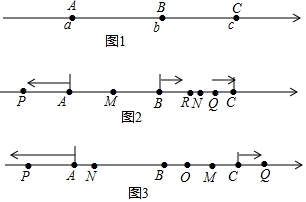 如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20.
如图,已知数轴上有三点A、B、C,它们对应的数分别为a,b,c,且c-b=b-a,点C对应的数是20. 已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )
已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )