Question

11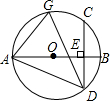．如图，AB是⊙O的直径，弦CD⊥AB于点E，G是$\widehat{AC}$上任意一点，连结AD，GD．$\widehat{BC}$=50°，则∠AGD=（　　）

• A． 50°
• B． 55°
• C． 65°
• D． 75°

Answer 1

分析 首先连接OC，BD，由$\widehat{BC}$=50°，根据弧与圆心角的关系，可求得∠BOC的度数，又由弦CD⊥AB，由垂径定理可得$\widehat{BC}$=$\widehat{BD}$，则可求得∠BAD的度数，又由AB是⊙O的直径，根据直径所对的圆周角是直角，可求得∠B的度数，然后由圆周角定理，求得答案．

解答 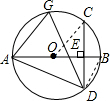解：连接OC，BD，
∵$\widehat{BC}$=50°，
∴∠BOC=50°，
∵弦CD⊥AB，
∴$\widehat{BC}$=$\widehat{BD}$，
∴∠BAD=$\frac{1}{2}$∠BOC=25°，
∵AB是⊙O的直径，
∴∠ADB=90°，
∴∠B=90°-∠BAD=65°，
∴∠AGD=∠B=65°．
故选C．

点评 此题考查了圆周角定理、垂径定理以及弧与圆心角的关系．注意准确作出辅助线是解此题的关键．