题目内容
已知a2+b2-
a-b+
=0,则a+b= .
| 1 |
| 2 |
| 5 |
| 16 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:将原等式化为a2-
a+
+b2-b+
=0,然后配方成完全平方的形式,利用非负数的性质求解即可.
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
解答:解:∵a2+b2-
a-b+
=0,
∴a2-
a+
+b2-b+
=0,
即:(a-
)2+(b-
)2=0,
∵(a-
)2≥0,(b-
)2≥0,
∴a-
=0,b-
=0,
解得:a=
,b=
,
∴a+b=
+
=
,
故答案为:
.
| 1 |
| 2 |
| 5 |
| 16 |
∴a2-
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
即:(a-
| 1 |
| 4 |
| 1 |
| 2 |
∵(a-
| 1 |
| 4 |
| 1 |
| 2 |
∴a-
| 1 |
| 4 |
| 1 |
| 2 |
解得:a=
| 1 |
| 4 |
| 1 |
| 2 |
∴a+b=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查配方这种基本的方法,在式子的变形中要注意变化前后式子的值不变.

练习册系列答案
相关题目
 如图,已知∠1=∠2,要说明△ABD≌△ACD还需要从下列条件中选一个,正确的说法是( )
如图,已知∠1=∠2,要说明△ABD≌△ACD还需要从下列条件中选一个,正确的说法是( )| A、∠B=∠C |
| B、∠ADB=∠ACD |
| C、DB=DC |
| D、AD=AD |




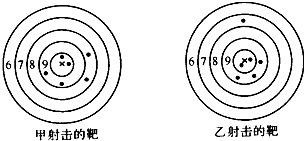 如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.