题目内容
12.计算:(1)$\sqrt{18}$-$\frac{2}{\sqrt{2}}$+|1-$\sqrt{2}$|
(2)1-$\frac{{x}^{2}-9}{{x}^{2}-6x+9}$÷$\frac{x+3}{x+4}$.
分析 (1)先化简,再进一步合并得出答案即可;
(2)先把分子分母因式分解,把除法改为乘法,进一步约分计算即可.
解答 (1)原式=3$\sqrt{2}$-$\sqrt{2}$+$\sqrt{2}$-1
=3$\sqrt{2}$-1;
(2)原式=1-$\frac{(x+3)(x-3)}{(x-3)2}$÷$\frac{x+3}{x+4}$
=1-$\frac{x+4}{x-3}$
=-$\frac{7}{x-3}$.
点评 此题考查二次根式的混合运算与分式的混合运算,掌握运算顺序与计算方法是解决问题的关键.

练习册系列答案
相关题目
7.关于x的方程$\frac{m-1}{x-1}$-$\frac{x}{x-1}$=0有增根,则m的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
17.下列根式中,是最简二次根式的为( )
| A. | $\sqrt{8a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{0.1x}$ | D. | $\sqrt{{a}^{5}}$ |
2.下列一元二次方程是一般形式的为( )
| A. | (x-1)2=0 | B. | 3x2-4x+1=0 | C. | x(x+5)=0 | D. | (x+6)2-9=0 |
 在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.
在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.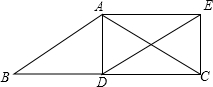 如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD. 如图,A是反比例函数y=$\frac{k}{x}$图象上一点,C是线段OA上一点,且OC:OA=1:3,作CD⊥x轴,垂足为点D,延长DC交反比例函数图象于点B,S△ABC=8,则k的值为9.
如图,A是反比例函数y=$\frac{k}{x}$图象上一点,C是线段OA上一点,且OC:OA=1:3,作CD⊥x轴,垂足为点D,延长DC交反比例函数图象于点B,S△ABC=8,则k的值为9.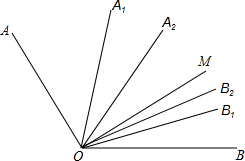 如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°.
如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°.