题目内容
将矩形ABCD折叠,使得对角线的两个端点A、C重合,折痕所在直线交直线AB于点E,如果AB=4,BE=1,则BC的长为 .
考点:翻折变换(折叠问题)
专题:分类讨论
分析:分类讨论:当点E在线段AB上,连结CE,根据折叠的性质得到AE=CE=3,然后在Rt△BCE中,利用勾股定理计算BC;当点E在线段AB的延长线上,连结CE,根据折叠的性质得AE=CE=5,在Rt△BCE中,根据勾股定理计算BC.
解答:解:当点E在线段AB上,如图1,连结CE,
∵AB=4,BE=1,
∴AE=3,
∵将矩形ABCD折叠,使得对角线的两个端点A、C重合,
∴AE=CE=3,
在Rt△BCE中,BC=
=
=2
;
当点E在线段AB的延长线上,如图2,连结CE,
 ∵AB=4,BE=1,
∵AB=4,BE=1,
∴AE=5,
∵将矩形ABCD折叠,使得对角线的两个端点A、C重合,
∴AE=CE=5,
在Rt△BCE中,BC=
=
=2
,
∴BC的长为2
或2
.
故答案为2
或2
.

∵AB=4,BE=1,
∴AE=3,
∵将矩形ABCD折叠,使得对角线的两个端点A、C重合,
∴AE=CE=3,
在Rt△BCE中,BC=
| CE2-BE2 |
| 32-12 |
| 2 |
当点E在线段AB的延长线上,如图2,连结CE,
 ∵AB=4,BE=1,
∵AB=4,BE=1,∴AE=5,
∵将矩形ABCD折叠,使得对角线的两个端点A、C重合,
∴AE=CE=5,
在Rt△BCE中,BC=
| CE2-BE2 |
| 52-12 |
| 6 |
∴BC的长为2
| 2 |
| 6 |
故答案为2
| 2 |
| 6 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
相关题目
 某校学生来自甲乙丙三个地区,其人数比为2:7:3,如图的扇形图表示上述分布情况.如果来自甲地区的有180人,则下列说法错误的是( )
某校学生来自甲乙丙三个地区,其人数比为2:7:3,如图的扇形图表示上述分布情况.如果来自甲地区的有180人,则下列说法错误的是( )| A、该校学生的总数是1080人 |
| B、扇形甲的圆心角是36° |
| C、该校来自乙地区的有630人 |
| D、扇形丙的圆心角是90° |
一个正比例函数的图象经过点(2,-5),它的表达式为( )
A、y=-
| ||
B、y=
| ||
C、y=
| ||
D、y=-
|
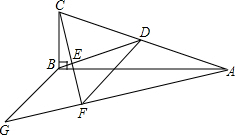 如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF
如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF 如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=110°,则∠2=
如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=110°,则∠2= 如图,在△ABC中,已知点D为BC的中点,点E、F分别为AD、BE的中点,若S△ABC=8,则S△CEF=
如图,在△ABC中,已知点D为BC的中点,点E、F分别为AD、BE的中点,若S△ABC=8,则S△CEF=