题目内容
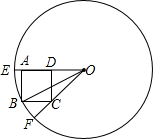 如图,已知圆O的直径为10cm,圆上有三点E、B、F,四边形ABCD为正方形,∠EOF=45°,求AB的长度?
如图,已知圆O的直径为10cm,圆上有三点E、B、F,四边形ABCD为正方形,∠EOF=45°,求AB的长度?考点:勾股定理,圆的认识
专题:计算题
分析:由四边形ABCD为正方形,得到四条边相等,再由题意得到三角形OCD为等腰直角三角形,得到OD=CD,在直角三角形AOB中,设AB=x,则有OA=2x,利用勾股定理求出x的值,即可确定出AB的长.
解答:解:∵四边形ABCD为正方形,∠EOF=45°,
∴AD=DC=AB=BC,△OCD为等腰直角三角形,
∴OD=CD,
设AD=OD=DC=AB=x,则有OA=OD+DA=2x,
在Rt△AOB中,根据勾股定理得:OB2=OA2+AB2,
即52=(2x)2+x2,
整理得:4x2+x2=25,
解得:x=
,
则AB=
.
∴AD=DC=AB=BC,△OCD为等腰直角三角形,
∴OD=CD,
设AD=OD=DC=AB=x,则有OA=OD+DA=2x,
在Rt△AOB中,根据勾股定理得:OB2=OA2+AB2,
即52=(2x)2+x2,
整理得:4x2+x2=25,
解得:x=
| 5 |
则AB=
| 5 |
点评:此题考查了勾股定理,以及圆的认识,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
刘谦的魔术表演风靡全国,小明也学起了刘谦的发明了一个魔术盒,当任意有理数对(a,b)进入其中时,会得到一个新的有理数:a-b2+1,例如:把(3,-2)放入其中,就会得到3-(-2)2+1=0,现将有理数对(0,-3)放入其中,则会得到( )
| A、10 | B、-9 | C、-8 | D、-7 |
 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )| A、15° | B、20° |
| C、25° | D、30° |
 有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.
有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明. 如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )
如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )



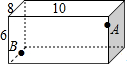 如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.
如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远. 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G