题目内容
17.甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得出现平局的情况,再利用概率公式求解即可求得答案.
解答 解:(1)画树状图得:
则共有9种等可能的结果;
(2)∵出现平局的有3种情况,
∴出现平局的概率为:$\frac{3}{9}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
7.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
| 小组 | 研究报告 | 小组展示 | 答辩 |
| 甲 | 91 | 80 | 78 |
| 乙 | 81 | 74 | 85 |
| 丙 | 79 | 83 | 90 |
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
5.下列计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | (x-y)2=x2-2xy-y2 | C. | (x+1)(x-1)=x2-1 | D. | (x-1)2=x2-1 |
2.某小组同学在一周内参加家务劳动时间与人数情况如表所示:
下列关于“劳动时间”这组数据叙述正确的是( )
| 劳动时间(小时) | 2 | 3 | 4 |
| 人数 | 3 | 2 | 1 |
| A. | 中位数是2 | B. | 众数是2 | C. | 平均数是3 | D. | 方差是0 |
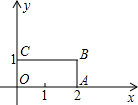 如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2).
如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2). 如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )


