题目内容
12.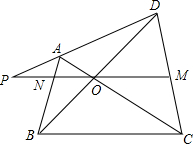 已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
分析 延长DP交CB的延长线于Q.由OP∥CQ,可得△APN∽△AQB,△AOP∽△ACQ,根据相似三角形对应边成比例得出PN:QB=AP:AQ=PO:QC,由比例的性质得出PN:PO=QB:QC.同理可得PO:PM=QB:QC,等量代换得到PN:PO=PO:PM,即PO2=PM•PN.
解答  证明:延长DP交CB的延长线于Q.
证明:延长DP交CB的延长线于Q.
∵OP∥CQ,
∴△APN∽△AQB,△AOP∽△ACQ,
∴PN:QB=AP:AQ=PO:QC,
∴PN:PO=QB:QC.
在△DQC范围内,∵MP∥CQ,
∴△DPO∽△DQB,△DPM∽△DQC,
∴PO:QB=DP:DQ=PM:QC,
∴PO:PM=QB:QC,
∴PN:PO=PO:PM,
∴PO2=PM•PN.
点评 本题考查了相似三角形的判定与性质,比例的性质,准确作出辅助线,证明出PN:PO=QB:QC以及PO:PM=QB:QC是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
4.绝对值小于3的所有整数的积等于( )
| A. | -36 | B. | 4 | C. | 0 | D. | 6 |
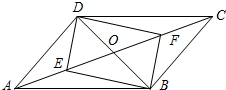 平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动
平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动