题目内容
2.解不等式$\frac{x+1}{6}-\frac{2x-5}{4}≥1$,并把解集在数轴上表示出来.分析 先根据不等式的性质求解不等式,然后把解集在数轴上表示出来.
解答 解:去分母得:2x+2-6x+15≥12,
移项、合并同类项得:-4x≥-5,
系数化为1得:x≤$\frac{5}{4}$.
在数轴上表示为: .
.
点评 本题考查了不等式的性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若|x-2|=2-x,则x的取值范围是( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |
14.一个多边形的每一个外角都等于40°,则这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
11.点M在第四象限,它到x轴,y轴的距离分别为4,3,则M坐标为( )
| A. | (3,-4) | B. | (4,-3) | C. | (-3,4) | D. | (-4,3) |
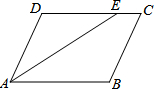 如图,在?ABCD中,∠DAB的角平分线交CD于E,若DE:EC=3:1,AB的长为8,则BC的长为6.
如图,在?ABCD中,∠DAB的角平分线交CD于E,若DE:EC=3:1,AB的长为8,则BC的长为6.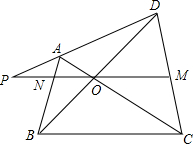 已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.