题目内容
20.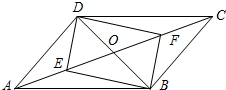 平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动
平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=18cm,当运动时间t为多少时,以D、E、B、F为顶点的四边形为矩形.
分析 (1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18-2t-2t=10,继而求得答案.
解答 解:(1)四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=2tcm或18-2tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC-AE-CF=BD或AE+CF-AC=EF,
∴18-2t-2t=10或2t+2t-18=10,
解得:t=2或t=7
∴当运动时间t为2s或7s时,四边形DEBF为矩形.
点评 此题考查了平行四边形的判定与性质以及矩形的判定,正确应用矩形的判定方法得出EF=BD是解题关键.

练习册系列答案
相关题目
11.点M在第四象限,它到x轴,y轴的距离分别为4,3,则M坐标为( )
| A. | (3,-4) | B. | (4,-3) | C. | (-3,4) | D. | (-4,3) |
15.已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,则此菱形的面积为( )
| A. | 48cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
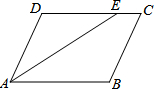 如图,在?ABCD中,∠DAB的角平分线交CD于E,若DE:EC=3:1,AB的长为8,则BC的长为6.
如图,在?ABCD中,∠DAB的角平分线交CD于E,若DE:EC=3:1,AB的长为8,则BC的长为6. 解决问题:
解决问题: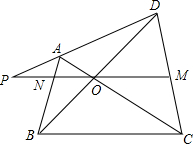 已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.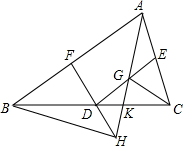 如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.
如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH. 如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?
如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?