Question

5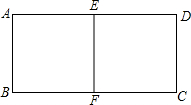．如图有一张矩形纸片，折成一半后形成的矩形与原矩形相似，则原矩形的长、宽的比是多少？

Answer 1

分析 根据相似多边形的对应边的比相等列出比例式，求出原矩形的长、宽的比．

解答 解：设AD=x，AB=y，
∵矩形ABCD∽矩形EABF，
∴$\frac{AB}{AE}$=$\frac{AD}{AB}$，即$\frac{y}{\frac{1}{2}x}$=$\frac{x}{y}$，
整理得，$\frac{{x}^{2}}{{y}^{2}}$=2，
则$\frac{x}{y}$=$\sqrt{2}$．
答：原矩形的长、宽的比是$\sqrt{2}$：1．

点评 本题考查的是相似多边形的性质，掌握相似多边形的性质为：对应角相等；对应边的比相等是解题的关键．