题目内容
16.已知,一元二次方程2x2+ax+(a-3)=0.(1)求证:不论a取任何实数,该方程都有两个不相等的实数根;
(2)已知x1,x2是该方程的两个根,且满足x12x2+x1x22=-2,求a的值.
分析 (1)表示出根的判别式,配方后得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;
(2)利用根与系数的关系可以得到x1+x2=-$\frac{a}{2}$,x1•x2=$\frac{1}{2}$(a-3),再把x12x2+x1x22=-2,变形为x1•x2(x1+x2)=-2,然后代入计算即可求解.
解答 证明:(1)△=a2-4×2(a-3)=a2-8a+24=(a-4)2+8,
∵(a-4)2≥0,
∴(a-4)2+8>0,
∴不论a取任何实数,该方程都有两个不相等的实数根;
(2)∵x1,x2是该方程的两个根,
∴x1+x2=-$\frac{a}{2}$,x1•x2=$\frac{1}{2}$(a-3),
∴x12x2+x1x22=x1•x2(x1+x2)=-$\frac{a}{4}$(a-3)=-2,
解得:a=$\frac{3+\sqrt{41}}{2}$或a=$\frac{3-\sqrt{41}}{2}$.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.以及根与系数的关系.

练习册系列答案
相关题目
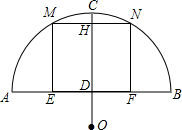 如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考)
如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考) 如图,已知AB=AC,OB=OC,∠ABO与∠ACO相等吗?为什么?
如图,已知AB=AC,OB=OC,∠ABO与∠ACO相等吗?为什么?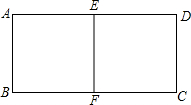 如图有一张矩形纸片,折成一半后形成的矩形与原矩形相似,则原矩形的长、宽的比是多少?
如图有一张矩形纸片,折成一半后形成的矩形与原矩形相似,则原矩形的长、宽的比是多少?