题目内容
12. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
分析 先根据OA=OB,∠BAO=25°得出∠B=25°,再由平行线的性质得出∠B=∠CAB=25°,根据圆周角定理即可得出结论.
解答 解:∵OA=OB,∠BAO=25°,
∴∠B=25°.
∵AC∥OB,
∴∠B=∠CAB=25°,
∴∠BOC=2∠CAB=50°.(同弧所对的圆心角等于圆周角的2倍)
故选B.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3. 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )
 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠1=∠2+∠3 | D. | ∠3=∠1+∠2 |
7.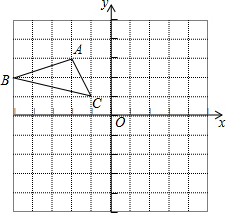 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )| A. | (-3,2) | B. | (2,-3) | C. | (1,-2) | D. | (-1,2) |
4.若分式$\frac{|x|-1}{x+1}$的值为零,则x的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
1.不等式6-4x≥3x-8的非负整数解为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
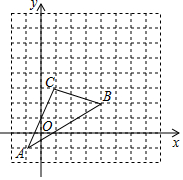 △ABC在直角坐标系中位置如图所示,把△ABC向右平移3个单位,再向上平移1个单位得△A′B′C′.
△ABC在直角坐标系中位置如图所示,把△ABC向右平移3个单位,再向上平移1个单位得△A′B′C′.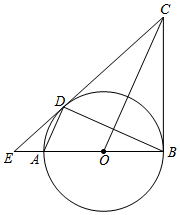 如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.