题目内容
13.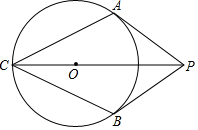 如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
分析 (1)连接AO,BO,根据PA、PB是⊙O的切线,得到∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=$\frac{1}{2}$∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;
(2)连接AB交PC于D,根据菱形的性质得到AD⊥PC,解直角三角形即可得到结论.
解答 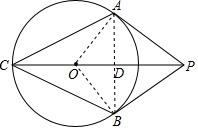 解:(1)连接AO,BO,
解:(1)连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=$\frac{1}{2}$∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=$\frac{\sqrt{3}}{2}$OA=$\frac{\sqrt{3}}{2}$,
∴PD=$\frac{3}{2}$,
∴PC=3,AB=$\sqrt{3}$,
∴菱形ACBP的面积=$\frac{1}{2}$AB•PC=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了切线的性质,菱形的判定和性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
3. 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )
 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠1=∠2+∠3 | D. | ∠3=∠1+∠2 |
4.若分式$\frac{|x|-1}{x+1}$的值为零,则x的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
1.不等式6-4x≥3x-8的非负整数解为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
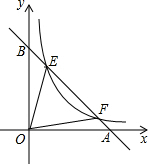 如图,点E、F在函数y=$\frac{2}{x}$的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是$\frac{8}{3}$.
如图,点E、F在函数y=$\frac{2}{x}$的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是$\frac{8}{3}$.