题目内容
18．
如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（-3，4），B（-5，2），C（-2，1）．（1）画出△ABC关于y轴的对称图形△A1B1C1；
（2）画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2；
（3）求（2）中线段OA扫过的图形面积．
分析 （1）分别作出各点关于y轴的对称点，再顺次连接即可；
（2）根据图形旋转的性质画出旋转后的图形△A2B2C2即可；
（3）利用扇形的面积公式即可得出结论．
解答 
解：（1）如图，△A1B1C1即为所求；
（2）如图，△A2B2C2即为所求；
（3）∵OA=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴线段OA扫过的图形面积=$\frac{90π×{5}^{2}}{360}$=$\frac{25}{4}$π．
点评 本题考查的是作图-旋转变换，熟知图形旋转不变性的性质是解答此题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
8．将抛物线y=3x2向下、向左各平移1个单位，所得抛物线的解析式为（ ）
| A． | y=3（x-1）2-1 | B． | y=3（x+1）2-1 | C． | y=3（x-1）2+1 | D． | y=3（x+1）2+1 |
9．在Rt△ABC中，∠C=90°，AB=4，AC=1，则cosB的值为（ ）
| A． | $\frac{\sqrt{15}}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{\sqrt{15}}{15}$ | D． | $\frac{4\sqrt{17}}{17}$ |
6．作为“一带一路”倡议的重大先行项目，中国、巴基斯坦经济走廊建设进展快、成效显著．两年来，已有18个项目在建或建成，总投资额达185亿美元．185亿用科学记数法表示为（ ）
| A． | 1.85×109 | B． | 1.85×1010 | C． | 1.85×1011 | D． | 1.85×1012 |
3．
如右图，AB∥CD，则下列式子一定成立的是（ ）
如右图，AB∥CD，则下列式子一定成立的是（ ）| A． | ∠1=∠3 | B． | ∠2=∠3 | C． | ∠1=∠2+∠3 | D． | ∠3=∠1+∠2 |
7．
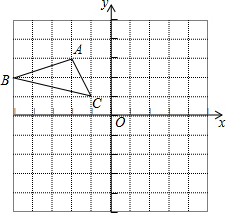如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是（-2，3），先把△ABC向右平移4个单位长度得到△A1B1C1，再作与△A1B1C1关于x轴对称的△A2B2C2，则点A的对应点A2的坐标是（ ）
如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是（-2，3），先把△ABC向右平移4个单位长度得到△A1B1C1，再作与△A1B1C1关于x轴对称的△A2B2C2，则点A的对应点A2的坐标是（ ）| A． | （-3，2） | B． | （2，-3） | C． | （1，-2） | D． | （-1，2） |
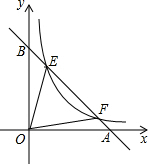如图，点E、F在函数y=$\frac{2}{x}$的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是$\frac{8}{3}$．