题目内容
9. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,EF=2,则△CEF的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,EF=2,则△CEF的周长为( )| A. | 8 | B. | 9.5 | C. | 10 | D. | 11.5 |
分析 直接利用平行四边形的性质结合角平分线的性质得出∠CEF=∠CFE,∠BAE=∠AEB,进而求出EC=FC的长即可得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠DAE=∠AEB,∠BAF=∠DFA,∠DAF=∠CEF,
∵∠BAD的平分线交BC于点E,交DC的延长线于点F,
∴∠BAF=∠DAF,
∴∠CEF=∠CFE,∠BAE=∠AEB,
∴EC=FC,AB=BE=6,
∵AD=BC=9,
∴EC=FC=3,
∴△CEF的周长为:EC+FC+EF=8.
故选:A.
点评 此题主要考查了平行四边形的性质以及角平分线的性质等知识,得出∠CEF=∠CFE,∠BAE=∠AEB是解题关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
17. 如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )
如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )
 如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )
如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )| A. | 12 | B. | 18 | C. | 20 | D. | 36 |
14.有一满池水,池底有泉水总能均匀地向外漏流,已知用24部A型抽水机,6天可抽干池水;若用21部A型抽水机8天也可抽干池水.设每部抽水机单位时间的抽水量相同,要使这一池水永远抽不干,则至多只能用( )部A型抽水机抽水.
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
20.小亮在匀速行驶的汽车里,注意到公路里程碑上的数如下:
则12:00时看到的两位数是27.
| 时刻 | 12:00 | 13:00 | 16:00 |
| 碑上的数 | 是一个两位数 | 十位与个位数字与12:00时 所看到的正好颠倒了 | 比12:00时看到的两位数 中间多了个0 |
 已知一次函数y=ax+b(a,b为常数)经过A(2,0)、B(0,1),求a,b.
已知一次函数y=ax+b(a,b为常数)经过A(2,0)、B(0,1),求a,b.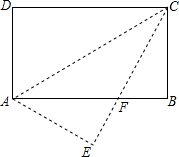 如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.
如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.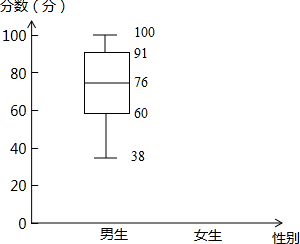 在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;
在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;