题目内容
已知x=
-1,求下列问题:
(1)证明:x2+2x=1;
(2)利用(1)的结论,化简x4+2x3+2x-1;
(3)试判断x=
-1是不是方程
-1=
的解?
| 2 |
(1)证明:x2+2x=1;
(2)利用(1)的结论,化简x4+2x3+2x-1;
(3)试判断x=
| 2 |
| 2x |
| x+1 |
| 1 |
| x2+4x+3 |
考点:二次根式的化简求值,分式方程的解
专题:计算题
分析:(1)已知等式变形后,两边平方,利用完全平方公式展开,变形即可得证;
(2)原式变形后,将(1)结论代入计算即可求出值;
(3)方程去分母,整理后将(1)结论代入即可做出判断.
(2)原式变形后,将(1)结论代入计算即可求出值;
(3)方程去分母,整理后将(1)结论代入即可做出判断.
解答:解:(1)已知等式变形得:x+1=
,两边平方得:(x+1)2=2,
整理得:x2+2x+1=2,即x2+2x=1;
(2)由(1)得x2+2x=1,
则原式=x2(x2+2x)+2x-1=x2+2x-1=1-1=0;
(3)方程去分母得:2x(x+3)-(x+3)(x+1)=-1,
去括号,整理得:x2+2x=2,
由(1)得:x2+2x=1,
则x=
-1不是原方程的解.
| 2 |
整理得:x2+2x+1=2,即x2+2x=1;
(2)由(1)得x2+2x=1,
则原式=x2(x2+2x)+2x-1=x2+2x-1=1-1=0;
(3)方程去分母得:2x(x+3)-(x+3)(x+1)=-1,
去括号,整理得:x2+2x=2,
由(1)得:x2+2x=1,
则x=
| 2 |
点评:此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.
如图,动直线y=kx(k>0)与抛物线y=ax2(a是常数,且a>0)相交与点O,A,以OA为边作矩形OABC.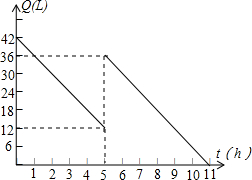 某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.
某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题. 如图,直线y=kx+b(k<0)交x轴于A(4,0),则关于x的不等式kx+b>0的解集为
如图,直线y=kx+b(k<0)交x轴于A(4,0),则关于x的不等式kx+b>0的解集为