题目内容
x2-3x+ =(x- )2;
x2-3x+
=
(x- )2.
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
考点:配方法的应用
专题:
分析:配方时加上一次项系数的绝对值的一半的平方即可;对于二次项系数不是1的应先提取二次项系数,然后配方.
解答:解:x2-3x+
=(x-
)2;
x2-3x+
=
(x2-6x+9)=
(x-3)2.
故答案为:
,
;3.
| 9 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 9 |
| 4 |
| 3 |
| 2 |
点评:考查了配方法的应用,解题的关键是了解如何进行配方,难度不大.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 已知:实数a、b在数轴上的位置如图所示,那么化简|a+b|-
已知:实数a、b在数轴上的位置如图所示,那么化简|a+b|-| (a-b)2 |
| A、2a | B、2b |
| C、-2a | D、-2b |
把(a-b)
根号外面的因式移到根号里面,化成最简二次根式,正确的结果是( )
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下列函数中,y随x的增大而增大的函数是( )
| A、y=-2x |
| B、y=-2x+1 |
| C、y=-2+x |
| D、y=-x-2 |


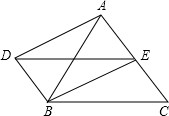 如图,DB∥AC,且DB=
如图,DB∥AC,且DB= 如图,EF∥AD,AD∥BC,∠1=∠2,∠DAC=120°,∠3=20°.求∠FEC的度数.
如图,EF∥AD,AD∥BC,∠1=∠2,∠DAC=120°,∠3=20°.求∠FEC的度数.