题目内容
 如图,在矩形ABCD中,点E在AB边上,点F在AD边上,且AE=DF,AF=CD,连接线段CE、EF、CF.点G是线段CE的中点,点M是线段EF上一点,过点G作GN⊥GM,将CF于点N.
如图,在矩形ABCD中,点E在AB边上,点F在AD边上,且AE=DF,AF=CD,连接线段CE、EF、CF.点G是线段CE的中点,点M是线段EF上一点,过点G作GN⊥GM,将CF于点N.(1)求证:△AEF≌△DFC;
(2)求证:ME=NF.
考点:矩形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用SAS即可证明;
(2)易证△EFC是等腰直角三角形,作GK⊥CF,GH⊥EF,分别于点K和H,证明△GHM≌△GKN即可证得.
(2)易证△EFC是等腰直角三角形,作GK⊥CF,GH⊥EF,分别于点K和H,证明△GHM≌△GKN即可证得.
解答: 证明:(1)∵AB=CD,AB=AE,
证明:(1)∵AB=CD,AB=AE,
∴AE=CD,
∵矩形ABCD,
∴∠A=∠D=90°,
在△AEF和△DCE中
,
∴△AEF≌△DCE;
(2)∵△AEF≌△DCE,
∴∠AFE=∠DCF,∠DFC=∠AEF,EF=FC,
又∵直角△AEF中,∠DFC+∠DCF=90°,
∴∠AFE+∠DFC=90°,
∴∠EFC=90°,
∴△EFC是等腰直角三角形.
作GK⊥CF,GH⊥EF,分别于点K和H.
则四边形HGKF是矩形,
∴∠HGK=90°,
∵GN⊥GM,
∴∠HGM=∠NGK,
又∵点G是线段CE的中点,
∴HG=GK,EH=HF=FK=CK,
在△GHM和△GKN中,
,
∴△GHM≌△GKN,
∴HM=NK,
又∵EH=FK,
∴ME=NF.
 证明:(1)∵AB=CD,AB=AE,
证明:(1)∵AB=CD,AB=AE,∴AE=CD,
∵矩形ABCD,
∴∠A=∠D=90°,
在△AEF和△DCE中
|
∴△AEF≌△DCE;
(2)∵△AEF≌△DCE,
∴∠AFE=∠DCF,∠DFC=∠AEF,EF=FC,
又∵直角△AEF中,∠DFC+∠DCF=90°,
∴∠AFE+∠DFC=90°,
∴∠EFC=90°,
∴△EFC是等腰直角三角形.
作GK⊥CF,GH⊥EF,分别于点K和H.
则四边形HGKF是矩形,
∴∠HGK=90°,
∵GN⊥GM,
∴∠HGM=∠NGK,
又∵点G是线段CE的中点,
∴HG=GK,EH=HF=FK=CK,
在△GHM和△GKN中,
|
∴△GHM≌△GKN,
∴HM=NK,
又∵EH=FK,
∴ME=NF.
点评:本题综合考查了等腰直角三角形,等腰三角形的判定,矩形的性质,全等三角形的性质和判定等知识点,题型较好,难度不大,主要考查学生运用所学知识分析问题和解决问题的能力.

练习册系列答案
相关题目

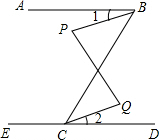 如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.
如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.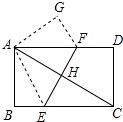 如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.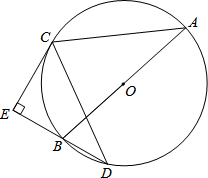 如图,AB为⊙O直径,C、D为⊙O上的点,CD=CA,CE⊥DB交DB的延长线于点E.
如图,AB为⊙O直径,C、D为⊙O上的点,CD=CA,CE⊥DB交DB的延长线于点E.