题目内容
 如图,在Rt△ABC中,∠B=90°,∠C=30°,点D、E、F分别在边BC、AB、AC上,联结DE、EF、FD,若BE=
如图,在Rt△ABC中,∠B=90°,∠C=30°,点D、E、F分别在边BC、AB、AC上,联结DE、EF、FD,若BE=| 1 |
| 2 |
(1)求证:四边形AEDF是平行四边形;
(2)若AC=3AE,求证:四边形AEDF是菱形.
考点:菱形的判定,平行四边形的判定
专题:
分析:(1)分别证明AB∥FD,ED∥AC可证明四边形AEDF是平行四边形;
(2)根据平行四边形的性质可得AE=FD,再根据直角三角形的性质可得AC=3AE,然后证明AF=FD,可得四边形AEDF是菱形.
(2)根据平行四边形的性质可得AE=FD,再根据直角三角形的性质可得AC=3AE,然后证明AF=FD,可得四边形AEDF是菱形.
解答:证明:(1)∵FD⊥BC,
∴∠FDC=90°,
∵∠B=90°,
∴AB∥FD,
∵BE=
ED,
∴sin∠EDB=
,
∴∠EDB=30°,
∵∠C=30°,
∴ED∥AC,
∴四边形AEDF是平行四边形;
(2)∵四边形AEDF是平行四边形,
∴AE=FD,
∵∠C=30°,
∴FD=
FC,
∵AC=3AE,
∴AE=
AC,
∴
FC=
AC,
∴3FC=2AC,
3FC=2(AF+FC),
3FC=2AF+2FC,
CF=2AF,
∴AF=FD,
∴四边形AEDF是菱形.
∴∠FDC=90°,
∵∠B=90°,
∴AB∥FD,
∵BE=
| 1 |
| 2 |
∴sin∠EDB=
| 1 |
| 2 |
∴∠EDB=30°,
∵∠C=30°,
∴ED∥AC,

∴四边形AEDF是平行四边形;
(2)∵四边形AEDF是平行四边形,
∴AE=FD,
∵∠C=30°,
∴FD=
| 1 |
| 2 |
∵AC=3AE,
∴AE=
| 1 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 3 |
∴3FC=2AC,
3FC=2(AF+FC),
3FC=2AF+2FC,
CF=2AF,
∴AF=FD,
∴四边形AEDF是菱形.
点评:此题主要考查了平行四边形的性质和判定,以及菱形的判定,关键是掌握两组对边分别平行的四边形是平行四边形,邻边相等的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算中正确的是( )
| A、(-ab)2=2a2b2 |
| B、(a+1)2=a2+1 |
| C、a6÷a2=a3 |
| D、(-x2)3=-x6 |
 如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则AD边的长为
如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则AD边的长为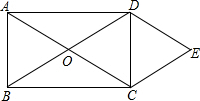 如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD. 如图是8×9的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.
如图是8×9的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.