题目内容
如图,在正方形网格中,每个小正方形的边长都是1,△ABC的顶点均在格点上,线段BC经过格点D,请用两种不同的方法说明△ABC是直角三角形.


考点:勾股定理的逆定理,勾股定理
专题:
分析:方法一:先由勾股定理,可求得AC2+BC2=AB2,然后根据勾股定理的逆定理,即可判定△ABC是直角三角形;
方法二:先证明△ACE≌△BDF,得出∠CAE=∠DBF,而由CE∥DF得出∠ECB=∠DBF,等量代换得到∠CAE=∠ECB,又∠CAE+∠ACE=90°,所以∠ECB+∠ACE=90°,即∠ACB=90°.
方法二:先证明△ACE≌△BDF,得出∠CAE=∠DBF,而由CE∥DF得出∠ECB=∠DBF,等量代换得到∠CAE=∠ECB,又∠CAE+∠ACE=90°,所以∠ECB+∠ACE=90°,即∠ACB=90°.
解答: 证明:△ABC是直角三角形.如图,
证明:△ABC是直角三角形.如图,
方法一:∵AC2=AE2+EC2=22+12=5,BC2=42+22=20,AB2=32+42=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°;
方法二:在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS),
∴∠CAE=∠DBF.
∵CE∥DF,
∴∠ECB=∠DBF,
∴∠CAE=∠ECB,
又∵∠CAE+∠ACE=90°,
∴∠ECB+∠ACE=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
 证明:△ABC是直角三角形.如图,
证明:△ABC是直角三角形.如图,方法一:∵AC2=AE2+EC2=22+12=5,BC2=42+22=20,AB2=32+42=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°;
方法二:在△ACE与△BDF中,
|
∴△ACE≌△BDF(SAS),
∴∠CAE=∠DBF.
∵CE∥DF,
∴∠ECB=∠DBF,
∴∠CAE=∠ECB,
又∵∠CAE+∠ACE=90°,
∴∠ECB+∠ACE=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
点评:此题考查了勾股定理,勾股定理的逆定理,全等三角形的判定与性质.解题的关键是掌握勾股定理与勾股定理的逆定理的应用,掌握数形结合思想的应用.

练习册系列答案
相关题目
下列属于尺规作图的是( )
| A、用刻度尺和圆规作△ABC |
| B、用量角器画一个300的角 |
| C、用圆规画半径2cm的圆 |
| D、作一条线段等于已知线段 |
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=42°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=42°,则∠C等于( )| A、30° | B、42° |
| C、48° | D、24° |
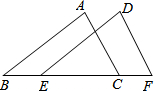 如图,在△ABC和△DEF中,B,E,C,F在同一条直线上,AB=DE,AC=DF,要使△ABC≌△DEF,还需要添加一个条件是( )
如图,在△ABC和△DEF中,B,E,C,F在同一条直线上,AB=DE,AC=DF,要使△ABC≌△DEF,还需要添加一个条件是( )| A、BE=CF |
| B、BE=EC |
| C、EC=CF |
| D、AC∥DF |
三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0的一个实数根,则该三角形的面积是( )
| A、24 | ||
| B、48 | ||
C、24或8
| ||
D、8
|