题目内容
已知直角坐标平面内的Rt△ABC三个顶点的坐标分别为A（1，2）、B（4，3）、C（3，-4），则直角顶点是 ．
考点：勾股定理的逆定理,两点间的距离公式
专题：
分析：首先根据两点间的距离公式求出AB2，BC2，AC2的值，然后根据勾股定理的逆定理即可确定该直角三角形的直角顶点．
解答：解：∵A（1，2）、B（4，3）、C（3，-4），
∴AB2=（4-1）2+（3-2）2=10，
BC2=（3-4）2+（-4-3）2=50，
AC2=（3-1）2+（-4-2）2=40，
∴BC2=AB2+AC2，
∴△ABC为直角三角形，∠A=90°．
故答案为A．
∴AB2=（4-1）2+（3-2）2=10，
BC2=（3-4）2+（-4-3）2=50，
AC2=（3-1）2+（-4-2）2=40，
∴BC2=AB2+AC2，
∴△ABC为直角三角形，∠A=90°．
故答案为A．
点评：本题主要考查勾股定理的逆定理、两点间的距离公式，关键在于正确的计算出AB2，BC2，AC2的值，正确的运用相关的定理、公式．
练习册系列答案
相关题目
如图，把正方形网格放在某平面直角坐标系内，点A的坐标为（-2，2），点B的坐标为（-1，-2），那么点C的坐标为
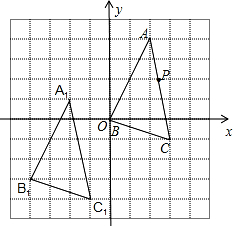在如图所示的直角坐标系中，△ABC经过平移后得到△A1B1C1（两个三角形的顶点都在格点上），已知在AC上一点P（2.4，2）平移后的对应点为P1，则P1点的坐标为（ ）| A、（-0.4，-1） |
| B、（-1.5，-1） |
| C、（-1.6，-1） |
| D、（-2.4，-2） |
如图，AB是⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D．
如图，小明用长为3m的竹竿CD作测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好在地面的同一点O，此时O点与竹竿的距离CD=6m，竹竿与旗杆的距离DB=12m，则旗杆AB的高为