题目内容
已知x=-1是关于x的方程2a+2=-1-bx的解.
(1)求代数式2a-b的值;
(2)求代数式5(2a-b)-2a+b+2的值.
(1)求代数式2a-b的值;
(2)求代数式5(2a-b)-2a+b+2的值.
考点:一元一次方程的解,代数式求值,整式的加减—化简求值
专题:
分析:(1)根据方程解的定义,把x=-1代入关于x的方程2a+2=-1-bx,即可得出代数式2a-b的值;
(2)把2a-b作为整体,代入代数式5(2a-b)-2a+b+2,求值即可.
(2)把2a-b作为整体,代入代数式5(2a-b)-2a+b+2,求值即可.
解答:解:(1)∵x=-1是关于x的方程2a+2=-1-bx的解,
∴2a+2=-1-b×(-1),
∴2a-b=-3;
(2)当2a-b=-3时,
原式=5(2a-b)-(2a-b)+2
=5×(-3)-(-3)+2
=-15+3+2
=-10.
∴2a+2=-1-b×(-1),
∴2a-b=-3;
(2)当2a-b=-3时,
原式=5(2a-b)-(2a-b)+2
=5×(-3)-(-3)+2
=-15+3+2
=-10.
点评:本题考查了一元一次方程的解,以及整式的加减,把2a-b作为整体,是数学中常用的整体思想.

练习册系列答案
相关题目
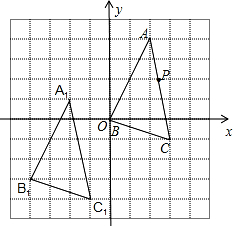 在如图所示的直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )
在如图所示的直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )| A、(-0.4,-1) |
| B、(-1.5,-1) |
| C、(-1.6,-1) |
| D、(-2.4,-2) |
 如图,BD是⊙O的直径,∠CBD=20°,则∠A的度数为( )
如图,BD是⊙O的直径,∠CBD=20°,则∠A的度数为( )| A、30° | B、45° |
| C、60° | D、70° |
函数y=
中,自变量x的取值范围是( )
| 1 | ||
|
| A、x≠2 | B、x≤2 |
| C、x>2 | D、x<2 |
已知点(-4,y1),(2,y2)都在直线y=-10x+2上,则y1,y2大小关系是( )
| A、y1>y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、不能比较 |

 如图,小明用长为3m的竹竿CD作测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离CD=6m,竹竿与旗杆的距离DB=12m,则旗杆AB的高为
如图,小明用长为3m的竹竿CD作测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离CD=6m,竹竿与旗杆的距离DB=12m,则旗杆AB的高为