题目内容
若|x+1|-|x-3|=2x-1,则x的值为 .
考点:含绝对值符号的一元一次方程
专题:
分析:分类讨论:x<-1,-1≤x<3,x≥3,根据分类,可化简去掉绝对值,根据解方程,可得答案.
解答:解:当x<-1时,原方程等价于-1-x-(3-x)=2x-1,解得x=-
当-1≤x<3时,原方程等价于1+x-(3-x)=2x-1,不存在实数解,
当x≥3时,原方程等价于x+1-(x-3)=2x-1,解得x=
(不符合题意的要舍去),
综上所述:x=-
,
故答案为:x=-
.
| 3 |
| 2 |
当-1≤x<3时,原方程等价于1+x-(3-x)=2x-1,不存在实数解,
当x≥3时,原方程等价于x+1-(x-3)=2x-1,解得x=
| 5 |
| 2 |
综上所述:x=-
| 3 |
| 2 |
故答案为:x=-
| 3 |
| 2 |
点评:本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
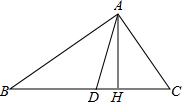 如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.
如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.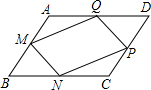 已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.
已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.