观察下列图形中点的个数.若按其规律再画下去.可以得到第5个图形中所有点的个数为( )A．16个B．25个C．36个D．49个题目和参考答案——青夏教育精英家教网—

题目内容

8．观察下列图形中点的个数，若按其规律再画下去，可以得到第5个图形中所有点的个数为（　　）

A．

16个

B．

25个

C．

36个

D．

49个

分析观察不难发现，点的个数依次为连续奇数的和，写出第n个图形中点的个数的表达式，再根据求和公式列式计算即可得解．

解答解：∵第1个图形中点的个数为：1+3=4，
第2个图形中点的个数为：1+3+5=9，
第3个图形中点的个数为：1+3+5+7=16，
…，
∴第n个图形中点的个数为：1+3+5+…+（2n+1）=（n+1）²．
∴第5个图形中所有点的个数为6²=36．
故选：C．

点评本题是对图形变化规律的考查，比较简单，观察出点的个数是连续奇数的和是解题的关键，还要注意求和公式的利用．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

11．解答下列问题．
（1）适合二元一次方程2x-y=4的解有多少组？请写出几组；
（2）适合二元一次方程x+y=5的解有多少组？请写出几组；
（3）找出一组x、y的值，使这组值同时适合方程2x-y=4和x+y=5；
（4）根据上面的探究，直接写出二元一次方程组$\left\{\begin{array}{l}{2x-y=4}\\{x+y=5}\end{array}\right.$的解，该方程组的解有多少组？

16．阅读下列学习内容：
（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠ABC=∠D=90°，E，F分别是BC、CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系．
探究思路如下：延长EB到点G，使BG=DF，连结AG．
$\left.\begin{array}{l}{AB=AD}\\{∠ABG=∠D}\\{BG=DF}\end{array}\right\}$⇒△ABG≌△ADF⇒$\left\{\begin{array}{l}{∠GAB=∠DAF}\\{AG=AF}\end{array}\right.$
$\left.\begin{array}{l}{∠BAD=120°}\\{∠EAF=60°}\end{array}\right\}$⇒∠DAF+∠BAE=60°⇒∠GAB+∠BAE=60°
∠EAG=60°⇒$\left.\begin{array}{l}{AE=AE}\\{∠FAE=∠EAG}\\{AF=AG}\end{array}\right\}$⇒△AEF≌△AEG⇒EF=EG
则由探究结果知，图中线段BE、EF、FD之间的数量关系为EF=BE+FD．
（2）根据上面的方法，解决问题：
如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=$\frac{1}{2}$∠BAD，
上述结论是否仍然成立，并说明理由；
（3）如图3，在四边形ABCD中，AB=BC=CD=DA，∠BAD=∠B=∠C=∠D=90°，点M、N分别在边BC、CD上，且∠MAN=45°，若BM=3，ND=2，请求出线段MN的长度．

3．已知3×9ⁿ×27ⁿ=3²¹，则（m³•n²）²÷（m²）³的结果的平方根是（　　）

13．

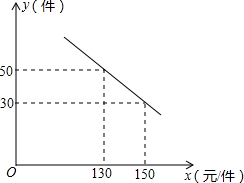某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系：
（1）求出y与x之间的函数关系式；
（2）写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
（3）该商场要求每天利润不能低于1200元，请写出销售价格x（元/件）的取值范围；若还需考虑销售量尽可能大，销售价格应订为多少元/件？

20．已知点A（0，4），B点在x轴上，线段AB与坐标轴围成三角形的面积为2，则B点坐标为（　　）

17．用适当的方法解下列方程．
（1）x²-2x-2=0
（2）（x-5）（x+2）=8
（3）x（2x-3）=（3x+2）（2x-3）
（4）（x-1）²-2（x²-1）=0
（5）2x²+1=2$\sqrt{3}$x
（6）3x²+5（2x+1）=0．

18．

如图，AB是⊙O的弦，半径OA=20cm，∠AOB=120°．求：
①△OAB的面积．
②阴影部分的面积．（精确到1cm²）

试题分类