题目内容
12. 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
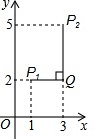
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).已知点A($-\frac{1}{2}$,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值.
分析 ①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0-y|=2,据此可以求得y的值;
②设点B的坐标为(0,y).因为|-$\frac{1}{2}$-0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-$\frac{1}{2}$-0|=$\frac{1}{2}$.
解答 解:①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|-$\frac{1}{2}$-0|=$\frac{1}{2}$≠2,
∴|0-y|=2,
解得,y=2或y=-2;
∴点B的坐标是(0,2)或(0,-2);
②点A与点B的“非常距离”的最小值为$\frac{1}{2}$.
点评 此题考查坐标与图形的特征,理解题意,掌握“非常距离”的求法是解决问题的关键.

练习册系列答案
相关题目
17.用-x表示的数一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 无法确定 |
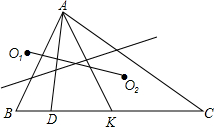 设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.
设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.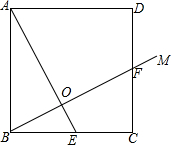 已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.