题目内容
1.计算下列各式,然后解答后面的问题:(1)($\sqrt{2}$+1)($\sqrt{2}$-1)=1.($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=1;($\sqrt{4}$+$\sqrt{3}$)($\sqrt{4}$-$\sqrt{3}$)=1;($\sqrt{5}$+$\sqrt{4}$)($\sqrt{5}$-$\sqrt{4}$)=1,…
(2)观察上面的规律,计算下列式子的值
$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1 $\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$ $\frac{1}{\sqrt{4}+\sqrt{3}}$=2-$\sqrt{3}$.
猜想:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$
根据上面规律计算:
($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$•($\sqrt{2013}$+1)
(3)拓展应用,试比较$\sqrt{12}$-$\sqrt{11}$与$\sqrt{13}$-$\sqrt{12}$的大小.
分析 (1)原式利用平方差公式计算即可得到结果;
(2)归纳总结得到一般性规律,写出即可;
(3)两数利用得出的规律变形,比较即可.
解答 解:(1)($\sqrt{2}$+1)($\sqrt{2}$-1)=2-1=1;($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=3-2=1;($\sqrt{4}$+$\sqrt{3}$)($\sqrt{4}$-$\sqrt{3}$)=4-3=1;($\sqrt{5}$+$\sqrt{4}$)($\sqrt{5}$-$\sqrt{4}$)=5-4=1;
(2)$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1;$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$;$\frac{1}{\sqrt{4}+\sqrt{3}}$=2-$\sqrt{3}$;$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(3)$\sqrt{12}$-$\sqrt{11}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,$\sqrt{13}$-$\sqrt{12}$=$\frac{1}{\sqrt{13}+\sqrt{12}}$,
∵$\sqrt{12}$+$\sqrt{11}$<$\sqrt{13}$+$\sqrt{12}$,
∴$\frac{1}{\sqrt{12}+\sqrt{11}}$>$\frac{1}{\sqrt{13}+\sqrt{12}}$,
则$\sqrt{12}$-$\sqrt{11}$>$\sqrt{13}$-$\sqrt{12}$.
故答案为:(1)1;1;1;1;(2)$\sqrt{2}$-1;$\sqrt{3}$-$\sqrt{2}$;2-$\sqrt{3}$;$\sqrt{n+1}$-$\sqrt{n}$
点评 此题考查了分母有理化,以及实数大小比较,熟练掌握运算法则是解本题的关键.

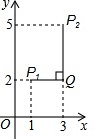 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
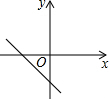
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义: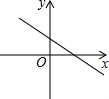 一次函数y=ax-b的图象如图,则y=bx-a的图象可能是( )
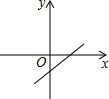
一次函数y=ax-b的图象如图,则y=bx-a的图象可能是( )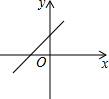
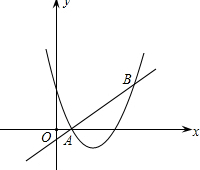 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).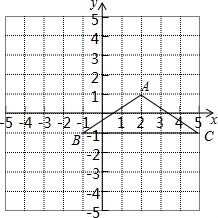 三角形ABC在平面直角坐标系中的位置如图所示.
三角形ABC在平面直角坐标系中的位置如图所示.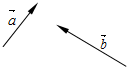 如图,已知两个不平行的向量$\overrightarrow{a}$、$\overrightarrow{b}$.先化简,再求作:(4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$)-2($\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$)(不要求写作法,但要指出图中表示结论的向量)
如图,已知两个不平行的向量$\overrightarrow{a}$、$\overrightarrow{b}$.先化简,再求作:(4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$)-2($\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$)(不要求写作法,但要指出图中表示结论的向量)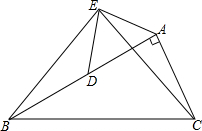 如图,在Rt△ABC中,∠BAC=90°,AB=2AC,点D是AB的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合(与Rt△ABC在同一平面内),连接BE,EC.试猜想线段BE和EC的数量及位置关系,并对你的猜想说明理由.
如图,在Rt△ABC中,∠BAC=90°,AB=2AC,点D是AB的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合(与Rt△ABC在同一平面内),连接BE,EC.试猜想线段BE和EC的数量及位置关系,并对你的猜想说明理由.