题目内容
17. 细心观察图,认真分析各式,然后解答问题:
细心观察图,认真分析各式,然后解答问题:($\sqrt{1}$)2+1=2,S1=$\frac{\sqrt{1}}{2}$
($\sqrt{2}$)2+1=3,S2=$\frac{\sqrt{2}}{2}$
($\sqrt{3}$)2+1=4,S3=$\frac{\sqrt{3}}{2}$
(1)用含n(n是正整数)的等式表示上述变化规律;
(2)计算S12+S22+S32+S42+…+S102的值.
分析 (1)直接根据题中给出的例子找出规律即可;
(2)根据(1)中的规律可得出结论.
解答 解:(1)由题意可知,($\sqrt{n}$)2+1=n+1,Sn=$\frac{\sqrt{n}}{2}$;
(2)∵Sn=$\frac{\sqrt{n}}{2}$,
∴S12+S22+S32+S42+…+S102=($\frac{\sqrt{1}}{2}$)2+($\frac{\sqrt{2}}{2}$)2+($\frac{\sqrt{3}}{2}$)2+…+($\frac{\sqrt{10}}{2}$)2
=$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$+…+$\frac{10}{4}$
=$\frac{55}{4}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
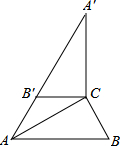 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,求AA′的长.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,求AA′的长.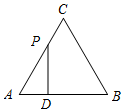 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )
如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )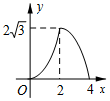
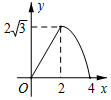
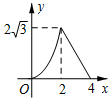
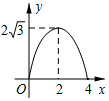
 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数.