题目内容
x,y都是质数,则方程x+y=1999共有( )
| A、1组解 | B、2组解 |
| C、3组解 | D、4组解 |
考点:质数与合数
专题:
分析:根据数字奇偶性得出1999只能分为:偶数+奇数,偶数质数只有2,即可得出答案.
解答:解:因为x+y=1999,
1999只能分为:偶数+奇数,
偶数质数只有2,
∵1999-2=1997,
∴只有两组解,
x=2,y=1997,
或x=1997,y=2.
故选:B.
1999只能分为:偶数+奇数,
偶数质数只有2,
∵1999-2=1997,
∴只有两组解,
x=2,y=1997,
或x=1997,y=2.
故选:B.
点评:此题主要考查了质数与合数,根据已知得出偶数质数只有2进而得出是解题关键.

练习册系列答案
相关题目
若方程x2+px-q=0的二根为x1,x2且x1>1,p+q+3>0,则x2( )
| A、小于1 | B、等于1 |
| C、大于1 | D、不能确定 |
 如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )
如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )| A、30° | B、40° |
| C、45° | D、60° |
已知反比例函数y=
的图象上有两点A(2,y1)、B(4,y2).则y1与y2的大小关系为( )
| 2 |
| x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、不能确定 |
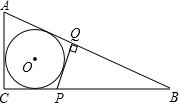 如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )