题目内容
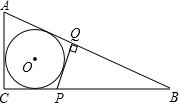 如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:三角形的内切圆与内心
专题:压轴题
分析:设⊙O的半径是R,PE=PF=x,BQ=y,连接OD,OG,OF,OE,得出正方形CDOE和OGQF,推出OD=CD=CE=OE=GQ=QF=R,求出y=2R,x=
R,根据锐角三角函数值求出即可.
| 1 |
| 2 |
解答:解:
设⊙O的半径是R,PE=PF=x,BQ=y,
连接OD,OG,OF,OE,
∵⊙O内切于Rt△ABC,
∴∠ODC=∠OEC=90°=∠C,AD=AG,
∵OD=OE,
∴四边形CDOE是正方形,
∴OD=CD=CE=OE=R,
同理OG=GQ=FQ=OF=R,
则PQ=CP,AC=AQ,
∵PQ⊥AB,∠C=90°,
∴∠C=∠PQB=90°,
∵∠B=∠B,
∴△BQP∽△BCA,
∴
=
=
,
∴BC=2BQ=2y,
根据BG=BE得:y+R=2y-R,
解得:y=2R,
在Rt△PQB中,由勾股定理得:PQ2+BQ2=BP2,
即(2R)2+(R+x)2=(4R-R-x)2,
解得:x=
R,
即PQ=
R+R=
R,BQ=2R,
tanB=
=
=
.
故选C.

设⊙O的半径是R,PE=PF=x,BQ=y,
连接OD,OG,OF,OE,
∵⊙O内切于Rt△ABC,
∴∠ODC=∠OEC=90°=∠C,AD=AG,
∵OD=OE,
∴四边形CDOE是正方形,
∴OD=CD=CE=OE=R,
同理OG=GQ=FQ=OF=R,
则PQ=CP,AC=AQ,
∵PQ⊥AB,∠C=90°,
∴∠C=∠PQB=90°,
∵∠B=∠B,
∴△BQP∽△BCA,
∴
| BQ |
| BC |
| PQ |
| AC |
| 1 |
| 2 |
∴BC=2BQ=2y,
根据BG=BE得:y+R=2y-R,
解得:y=2R,
在Rt△PQB中,由勾股定理得:PQ2+BQ2=BP2,
即(2R)2+(R+x)2=(4R-R-x)2,
解得:x=
| 1 |
| 2 |
即PQ=
| 1 |
| 2 |
| 3 |
| 2 |
tanB=
| PQ |
| BQ |
| ||
| 2R |
| 3 |
| 4 |
故选C.
点评:本题考查了正方形的性质和判定,切线的性质,勾股定理,相似三角形的性质和判定,切线长定理等知识点的应用,主要考查学生的推理和计算能力,难度偏大.

练习册系列答案
相关题目
x,y都是质数,则方程x+y=1999共有( )
| A、1组解 | B、2组解 |
| C、3组解 | D、4组解 |
 已知如图,按要求画图
已知如图,按要求画图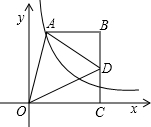 如图,点A在双曲线y=
如图,点A在双曲线y=
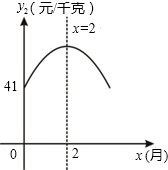 已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:
已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示: 小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据:
小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据: