题目内容
2.四边形ABCD的对角线AC、BD相交于O,若BD=6,AC=8,∠BOC=135°,则四边形ABCD的面积为12$\sqrt{2}$.分析 设OD=a,OB=b,OA=c,OC=d,则a+b=6,c+d=8,根据已知求得∠COD=∠AOB=45°,然后根据S四边形ABCD=S△AOD+S△AOB+S△BOC+S△COD=$\frac{1}{2}$ac•sin45°+$\frac{1}{2}$bc•sin45°+$\frac{1}{2}$bd•sin45°+$\frac{1}{2}$ad•sin45°即可求得.
解答 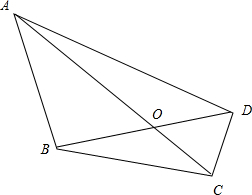 解:设OD=a,OB=b,OA=c,OC=d,则a+b=6,c+d=8,
解:设OD=a,OB=b,OA=c,OC=d,则a+b=6,c+d=8,
∵∠BOC=135°,
∴∠COD=∠AOB=45°,
∴S四边形ABCD=S△AOD+S△AOB+S△BOC+S△COD=$\frac{1}{2}$ac•sin45°+$\frac{1}{2}$bc•sin45°+$\frac{1}{2}$bd•sin45°+$\frac{1}{2}$ad•sin45°=$\frac{\sqrt{2}}{4}$(ac+bc+bd+ad)=$\frac{\sqrt{2}}{4}$(a+b)(c+d)=$\frac{\sqrt{2}}{4}$×6×8=12$\sqrt{2}$.
故答案为12$\sqrt{2}$.
点评 本题考查了三角形的面积,解直角三角函数,通过解直角三角函数求得三角形的高是解题的关键.

练习册系列答案
相关题目
13.下列说法中:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤画射线OA=3cm;⑥经过三点中的两点作直线总共有3条.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.在平行四边形ABCD中,∠A+∠C=240°,则∠B的度数是( )
| A. | 120° | B. | 80° | C. | 100° | D. | 60° |
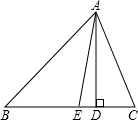 已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.
已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.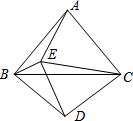 如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.
如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.