题目内容
10.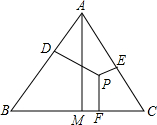 已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.
已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.
分析 连接PA,PB,PC,由S△ABC=S△PAC+S△PBC+S△PAB,可得$\frac{1}{2}$BC•h=$\frac{1}{2}$AB•h1+$\frac{1}{2}$AC•h2+$\frac{1}{2}$BC•h3,又由△ABC是等边三角形,即可得h=h1+h2+h3.
解答  解:h=h1+h2+h3,理由如下:
解:h=h1+h2+h3,理由如下:
连接PA,PB,PC,
则S△ABC=S△PAC+S△PBC+S△PAB,
∴$\frac{1}{2}$BC•h=$\frac{1}{2}$AB•h1+$\frac{1}{2}$AC•h2+$\frac{1}{2}$BC•h3,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴h=h1+h2+h3.
点评 此题考查了等边三角形的性质与三角形面积的求解方法.此题难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
20.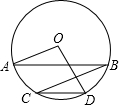 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )| A. | 120° | B. | 140° | C. | 110° | D. | 100° |
15.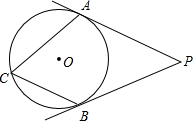 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )| A. | 50° | B. | 65° | C. | 75° | D. | 130° |
2.四名运动员参加了射击预选赛,他们成绩的平均环数$\overline{x}$及其方差s2如下表所示,
如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.3 | 9.2 | 9.2 | 8.5 |
| s2 | 1 | 1 | 1.2 | 1.7 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |
20.在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )
| A. | m>3 | B. | m<2 | C. | 2<m<3 | D. | m<3 |