题目内容
20.在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )| A. | m>3 | B. | m<2 | C. | 2<m<3 | D. | m<3 |
分析 根据第三象限的点的横坐标与纵坐标都是负数列出不等式组,然后求解即可.
解答 解:∵点(m-2,m-3)在第三象限,
∴$\left\{\begin{array}{l}{m-2<0}\\{m-3<0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m<2}\\{m<3}\end{array}\right.$
∴m<2.
故选:B.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
11.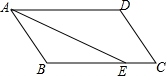 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A. | 4和1 | B. | 1和4 | C. | 3和2 | D. | 2和3 |
12. 如图是六个相同的小正方体组成的几何体,其左视图是( )
如图是六个相同的小正方体组成的几何体,其左视图是( )
 如图是六个相同的小正方体组成的几何体,其左视图是( )
如图是六个相同的小正方体组成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
10.下列计算正确的是( )
| A. | a5•a2=3a7 | B. | a4+a4=a8 | C. | (a3)3=a6 | D. | a5÷a2=a3 |
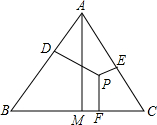 已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.
已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.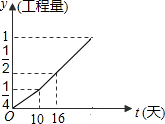 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.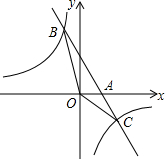 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5)、C($\frac{5}{2}$,d)两点.