题目内容
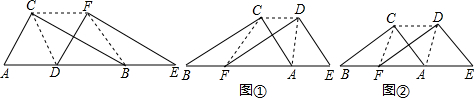
 某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°,已知原楼梯DB长为6cm,调整后的楼梯所占地面CD有多长?
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°,已知原楼梯DB长为6cm,调整后的楼梯所占地面CD有多长?(结果精确到0.1cm,参考数据:sin40°≈0.64,cos40°≈0.77,sin35°≈0.57,tan35°≈0.70)
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:根据原楼梯的倾斜角为40°,可先求出AD的长,继而在Rt△ACD中求出CD的长.
解答:解:在Rt△ABD中,
∵sin40°=
=
,
∴AD=5sin40°=6×0.64=3.84,
在Rt△ACD中,
∵tan35°=
,
∴CD=
≈5.5.
答:调整后的楼梯所占地面CD为5.5m.
∵sin40°=
| AD |
| AB |
| AD |
| 5 |
∴AD=5sin40°=6×0.64=3.84,
在Rt△ACD中,
∵tan35°=
| AD |
| CD |
∴CD=
| 3.84 |
| 0.7 |
答:调整后的楼梯所占地面CD为5.5m.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡度和坡角构造直角三角形,利用三角函数求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目