题目内容
图①是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.
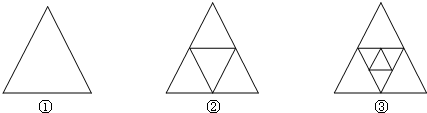
(1)图②有 个三角形;图③有 个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形?(用n的代数式表示结论)
(3)能否分出246个三角形?简述你的理由.

(1)图②有
(2)按上面的方法继续下去,第n个图形中有多少个三角形?(用n的代数式表示结论)
(3)能否分出246个三角形?简述你的理由.
考点:规律型:图形的变化类
专题:
分析:(1)可直接通过图形写出三角形的个数;
(2)本题可分别写出n=1,2,3…时所对应的三角形个数,找出有关于n的代数式;
(3)列方程计算,n必须是整数才可能,否则不可能.
(2)本题可分别写出n=1,2,3…时所对应的三角形个数,找出有关于n的代数式;
(3)列方程计算,n必须是整数才可能,否则不可能.
解答:解:(1)图②中有5个三角形,图③中有9个三角形.
(2)依题意得:n=1时,有1个三角形;
n=2时,有5个三角形;
n=3时,有9个三角形;
…
∴当n=n时有4n-3个三角形.
(3)假设存在正整数n,使得第n个图形中有246个三角形,根据题意得:4n-3=246
解得:n=
故不存在正整数n,使得第n个图形中有246个三角形
(2)依题意得:n=1时,有1个三角形;
n=2时,有5个三角形;
n=3时,有9个三角形;
…
∴当n=n时有4n-3个三角形.
(3)假设存在正整数n,使得第n个图形中有246个三角形,根据题意得:4n-3=246
解得:n=
| 249 |
| 4 |
故不存在正整数n,使得第n个图形中有246个三角形
点评:此题考查了图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出规律,解决问题.

练习册系列答案
相关题目
 如图,已知⊙O1的半径为6cm,⊙O2的半径为8cm,O1O2=10cm,两圆交于A、B两点,求AB的长.
如图,已知⊙O1的半径为6cm,⊙O2的半径为8cm,O1O2=10cm,两圆交于A、B两点,求AB的长. 如图,在?ABCD中,连结AC交BD于点O,过点O任作线段EF、GH,分别交DC、AB、DA、CB于点E、F、G、H.
如图,在?ABCD中,连结AC交BD于点O,过点O任作线段EF、GH,分别交DC、AB、DA、CB于点E、F、G、H. 某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°,已知原楼梯DB长为6cm,调整后的楼梯所占地面CD有多长?
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°,已知原楼梯DB长为6cm,调整后的楼梯所占地面CD有多长?