题目内容
19.已知a、b互为倒数,c、d互为相反数,有理数m所表示的点到2所对应的点的距离是3个单位长度,求:$\frac{ab}{5}$+$\frac{31}{197}×(c+d)$-m的值.分析 利用相反数以及倒数和数轴的性质得出m的值以及ab=1,c+d=0,进而代入求出即可.
解答 解:由题意得ab=1,c+d=0,m=5或-1,
当m=5时,原式=$\frac{1}{5}$+0-5=-$\frac{24}{5}$,
当m=-1时,原式=$\frac{1}{5}$+0+1=1$\frac{1}{5}$.
点评 此题主要考查了代数式求值、以及相反数和倒数的性质,正确掌握相关性质是解题关键.

练习册系列答案
相关题目
9.绝对值不大于2的整数有( )个.
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
7. 将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
 将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )| A. | 59.45° | B. | 60°15' | C. | 59°75' | D. | 59.75° |
8. 如图,AB∥CD,若∠2是∠1的3倍,则∠1的度数是( )
如图,AB∥CD,若∠2是∠1的3倍,则∠1的度数是( )
 如图,AB∥CD,若∠2是∠1的3倍,则∠1的度数是( )
如图,AB∥CD,若∠2是∠1的3倍,则∠1的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
9. 如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )
如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )
 如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )
如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )| A. | 80° | B. | 60° | C. | 45° | D. | 30° |
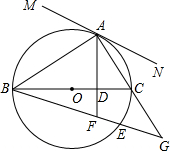 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G. 如图,直线AB与反比例函数的图象交于A(-4,2)、B(2,n)两点.
如图,直线AB与反比例函数的图象交于A(-4,2)、B(2,n)两点.