题目内容
4. 如图,直线AB与反比例函数的图象交于A(-4,2)、B(2,n)两点.
如图,直线AB与反比例函数的图象交于A(-4,2)、B(2,n)两点.(1)求反比例函数的解析式和直线AB的解析式;
(2)求△OAB的面积.
分析 (1)设反比例函数的解析式为y=$\frac{m}{x}$,把A(-4,2)代入y=$\frac{m}{x}$,求出m,即可得出反比例函数的表达式,把B(2,n)代入y=$\frac{m}{x}$,求出n,得出B的坐标,设直线AB的解析式y=kx+b,把A、B的坐标代入y=kx+b得出k和b即可;
(2)求出C的坐标,根据三角形的面积公式求出△AOC和△BOC的面积即可.
解答 解:(1)设反比例函数的解析式为y=$\frac{m}{x}$,
∵把A(-4,2)代入y=$\frac{m}{x}$得:m=-8,
∴反比例函数的表达式是y=-$\frac{8}{x}$,
把B(2,n)代入y=-$\frac{8}{x}$得:n=-4,
∴B的坐标是(2,-4),
把A、B的坐标代入y=kx+b得:$\left\{\begin{array}{l}{-4k+b=2}\\{2k+b=-4}\end{array}\right.$,
解得:k=-1,b=-2,
∴一次函数y=kx+b的表达式是y=-x-2;
(2)把y=0代入y=-x-2得:x=-2,
∴OC=2,
∵A(-4,2),B(2,-4),
∴△AOB的面积S=S△AOC+S△BOC=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×2=4.
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,三角形的面积,一次函数与反比例函数的交点问题等知识点的应用,用了数形结合思想.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
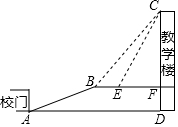 某山区为改善办学条件,依山新建一座教学楼,校门A处,有一坡度i=5:12的斜坡AB,在坡顶B处(铅直高度为10米)看教学楼CF的楼顶C的仰角∠CBF=53°,在E处仰角C的仰角∠CEF=63.4°,按规划要在离B点6米远的E处建一悬挂国旗的旗杆.
某山区为改善办学条件,依山新建一座教学楼,校门A处,有一坡度i=5:12的斜坡AB,在坡顶B处(铅直高度为10米)看教学楼CF的楼顶C的仰角∠CBF=53°,在E处仰角C的仰角∠CEF=63.4°,按规划要在离B点6米远的E处建一悬挂国旗的旗杆. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )
为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )