题目内容
14.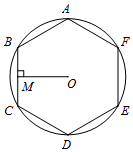 如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )
如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )| A. | 2$\sqrt{3}$、$\frac{4π}{3}$ | B. | 2$\sqrt{3}$、π | C. | $\sqrt{3}$、$\frac{2π}{3}$ | D. | 2、$\frac{π}{3}$ |
分析 连接OC、OB,证出△BOC是等边三角形,根据锐角三角函数的定义求解即可.
解答  解:如图所示,连接OC、OB
解:如图所示,连接OC、OB
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OA=OB,
∴△BOC是等边三角形,
∴∠OBM=60°,
∴OM=OBsin∠OBM=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
$\widehat{BC}$的长度=$\frac{60•π×4}{180}$=$\frac{4}{3}$π,
故选:A.
点评 题考查的是正六边形的性质、等边三角形的判定与性质、三角函数、弧长的计算;熟练掌握正六边形的性质,由三角函数求出OM是解决问题的关键.

练习册系列答案
相关题目
2.已知点(-2,a),(3,b)都在直线y=2x+m上,对于a,b的大小关系叙述正确的是( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a≤b |
6.贵州省3月份发布了2017年大数据十大工程,其中拟定了贵阳大数据交易所年度发展目标:交易会员达到2000家,交易规模累计300000000元人民币以上,将300000000这个数用科学记数法可表示为( )
| A. | 3×108 | B. | 0.3×108 | C. | 3×109 | D. | 0.3×109 |
1. 如图,已知AB∥CD,∠1=60°,则∠2=( )
如图,已知AB∥CD,∠1=60°,则∠2=( )
 如图,已知AB∥CD,∠1=60°,则∠2=( )
如图,已知AB∥CD,∠1=60°,则∠2=( )| A. | 90° | B. | 120° | C. | 60° | D. | 15° |
1.已知一个角的补角是80°48′,那么这个角的度数是( )
| A. | 9°12′ | B. | 10°48′ | C. | 99°12′ | D. | 100°48′ |
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.