题目内容
1. 如图,已知AB∥CD,∠1=60°,则∠2=( )
如图,已知AB∥CD,∠1=60°,则∠2=( )| A. | 90° | B. | 120° | C. | 60° | D. | 15° |
分析 根据平行线的性质得∠1=∠3=60°,再根据邻补角的定义得∠2+∠3=180°,则∠2=180°-60°=120°.
解答 解:如图,
∵AB∥CD,
∴∠1=∠3,
而∠1=60°,
∴∠3=60°,
又∵∠2+∠3=180°,
∴∠2=180°-60°=120°.
故选:B.
点评 本题考查了平行线的性质:两直线平行,同位角相等.也考查了邻补角的定义的运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.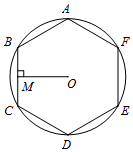 如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )
如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )
 如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )
如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM和弧BC的长分别为( )| A. | 2$\sqrt{3}$、$\frac{4π}{3}$ | B. | 2$\sqrt{3}$、π | C. | $\sqrt{3}$、$\frac{2π}{3}$ | D. | 2、$\frac{π}{3}$ |
5.山西的风景独特而优美,旅游资源精彩又丰富,文化旅游产业成为山西七大非煤产业之首.2015年,陕西省旅游总收入3447.5亿元,同比增长21.11%,旅游业已成为全省最具活力的产业之一,数据3447.5亿元用科学记数法可表示为( )
| A. | 34.475×1010元 | B. | 3.4475×1010元 | C. | 34.475×1011元 | D. | 3.4475×1011元 |
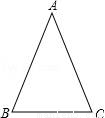
9. 如图,在正方形ABCD中,E是CD上的点,若BE=3,CE=1,则正方形ABCD的对角线的长为( )
如图,在正方形ABCD中,E是CD上的点,若BE=3,CE=1,则正方形ABCD的对角线的长为( )
 如图,在正方形ABCD中,E是CD上的点,若BE=3,CE=1,则正方形ABCD的对角线的长为( )
如图,在正方形ABCD中,E是CD上的点,若BE=3,CE=1,则正方形ABCD的对角线的长为( )| A. | 8 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4 |
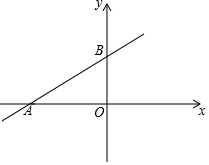 如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0).
如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0). 电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解答下列问题.
电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解答下列问题.