题目内容
13.计算(1)$\frac{3}{{\sqrt{3}}}$-($\sqrt{3}$)2+(π+$\sqrt{3}$)0-$\sqrt{27}$+|$\sqrt{3}$-2|
(2)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
(3)(2$\sqrt{5}$+$\sqrt{3}$)2-($\sqrt{5}$+$\sqrt{2}$)($\sqrt{5}$-$\sqrt{2}$)
(4)$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$+$\frac{2a-{a}^{2}}{a-2}$÷a.
分析 (1)先将各二次根式化简,然后合并同类二次根式即可.
(2)先将各二次根式化简,然后合并同类二次根式,最后利用二次根式除法法则即可求值
(3)根据完全平方公式和平方差公式展开后,合并同类项即可求值
(4)先将各分式的分子与分母进行因式分解,再根据分式的基本性质即可求值
解答 解:(1)原式=$\sqrt{3}$-3+1-3$\sqrt{3}$+2-$\sqrt{3}$=-3$\sqrt{3}$
(2)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$÷2$\sqrt{3}$
=$\frac{14}{3}$
(3)原式=(23+4$\sqrt{15}$)-(5-2)=20+4$\sqrt{15}$
(4)原式=$\frac{(a-1)(a+1)}{{(a-1)}^{2}}$+$\frac{a(2-a)}{a-2}$÷a
=$\frac{a+1}{a-1}$-1
=$\frac{2}{a-1}$
点评 本题考查学生的计算能力,解题的关键是熟练运算法则,本题属于基础题型.

练习册系列答案
相关题目
3.在下列调查中,适宜采用普查方式的是( )
| A. | 了解市民对马来西亚沉船事件的关注度 | |
| B. | 了解初三(1)班学生期末立定跳远成绩 | |
| C. | 为监测嘉陵江重庆段的物种生态情况 | |
| D. | 为掌握全国人民对王源联合国演讲的看法 |
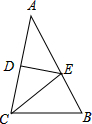 如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC的长是多少?
如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC的长是多少?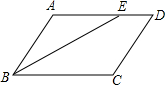 如图,?ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,?ABCD的周长20.
如图,?ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,?ABCD的周长20.