题目内容
 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.
考点:全等三角形的判定与性质,等边三角形的性质,扇形面积的计算
专题:
分析:(1)由点D是线段BC的中点得到BD=CD,再由AB=AC=BC可判断△ABC为等边三角形,于是得到AD为BC的垂直平分线,根据线段垂直平分线的性质得BE=CE;
(2)由EB=EC,根据等腰三角形的性质得∠EBC=∠ECB=30°,则根据三角形内角和定理计算得∠BEC=120°,在Rt△BDE中,BD=
BC=2,∠EBD=30°,根据含30°的直角三角形三边的关系得到ED=
BD=
,然后根据扇形的面积公式求解.
(2)由EB=EC,根据等腰三角形的性质得∠EBC=∠ECB=30°,则根据三角形内角和定理计算得∠BEC=120°,在Rt△BDE中,BD=
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
解答: (1)证明:∵点D是线段BC的中点,
(1)证明:∵点D是线段BC的中点,
∴BD=CD,
∵AB=AC=BC,
∴△ABC为等边三角形,
∴AD为BC的垂直平分线,
∴BE=CE;
(2)解:∵EB=EC,
∴∠EBC=∠ECB=30°,
∴∠BEC=120°,
在Rt△BDE中,BD=
BC=2,∠EBD=30°,
∴ED=BD•tan30°=
BD=
,
∴阴影部分(扇形)的面积=
=
π.
 (1)证明:∵点D是线段BC的中点,
(1)证明:∵点D是线段BC的中点,∴BD=CD,
∵AB=AC=BC,
∴△ABC为等边三角形,
∴AD为BC的垂直平分线,
∴BE=CE;
(2)解:∵EB=EC,
∴∠EBC=∠ECB=30°,
∴∠BEC=120°,
在Rt△BDE中,BD=
| 1 |
| 2 |
∴ED=BD•tan30°=
| ||
| 3 |
2
| ||
| 3 |
∴阴影部分(扇形)的面积=
120•π•(
| ||||
| 360 |
| 4 |
| 9 |
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.也考查了等边三角形的判定与性质、相等垂直平分线的性质以及扇形的面积公式.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,△ABC和△DEF的边BC、EF重叠的部分为FC,有下列四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠ACB=∠DFE.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:
如图,△ABC和△DEF的边BC、EF重叠的部分为FC,有下列四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠ACB=∠DFE.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设: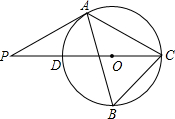 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,PA是⊙O的切线;
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,PA是⊙O的切线;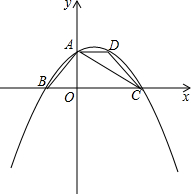 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
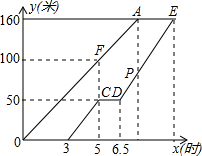 如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为
如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为