Question

10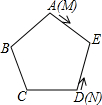．如图，M、N是正五边形ABCDE各边上的两个动点，若它们分别从顶点A、D出发，同时沿正五方形的边移动，M点以顺时针方向移动，N点以逆时针方向移动，假设点M的速度是点N的速度的5倍，则它们第2014次相遇在（　　）边上．

• A． AE
• B． ED
• C． CD
• D． AB

Answer 1

分析 设每边长为1，刚开始M、N之间的距离是2，M的速度是N的5倍，所以M走它们距离的$\frac{5}{6}$，也就是2×$\frac{5}{6}$=$\frac{5}{3}$，为整个图形周长的$\frac{1}{3}$，也就是第一次相遇在DE上，距离D$\frac{1}{3}$处，以此类推，第二次点N走的路程为5×$\frac{1}{6}$=$\frac{5}{6}$，此时点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$=$\frac{7}{6}$，相遇在AE上距离E$\frac{1}{6}$处，第三次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$=2，相遇在点A，第四次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$+$\frac{5}{6}$=2$\frac{5}{6}$，相遇在AB上距离B$\frac{1}{6}$处，第五次相遇点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×4=$\frac{11}{3}$，相遇在在BC上距离C$\frac{1}{3}$处，第六次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×5=$\frac{9}{2}$，相遇在相遇在CD中点处，第七次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×6=5$\frac{1}{3}$，相遇在相遇在第一次相遇处，所以6次一个循环从而不难求得它们第2014次相遇位置．

解答 解：设每边长为1，刚开始M、N之间的距离是2，M的速度是N的5倍，所以M走它们距离的$\frac{5}{6}$，也就是2×$\frac{5}{6}$=$\frac{5}{3}$，为整个图形周长的$\frac{1}{3}$，也就是第一次相遇在DE上，距离D$\frac{1}{3}$处，以此类推，第二次点N走的路程为5×$\frac{1}{6}$=$\frac{5}{6}$，此时点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$=$\frac{7}{6}$，相遇在AE上距离E$\frac{1}{6}$处，第三次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$=2，相遇在点A，第四次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$+$\frac{5}{6}$=2$\frac{5}{6}$，相遇在AB上距离B$\frac{1}{6}$处，第五次相遇点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×4=$\frac{11}{3}$，相遇在在BC上距离C$\frac{1}{3}$处，第六次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×5=$\frac{9}{2}$，相遇在相遇在CD中点处，第七次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×6=5$\frac{1}{3}$，相遇在相遇在第一次相遇处，所以6次一个循环；
2014÷6=335…4，
第2014次相遇点与第四次相遇在AB上．
故选：D．

点评 此题考查图形的变化规律，找出点在边上循环周期，得出6次一个循环是解决问题的关键．