题目内容
14.已知两组数据:甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7
分别计算这两组数据的众数,中位数,平均数,方差,并比较哪一个样本情况较稳定.
分析 先根据平均数的计算公式求出甲和乙数的平均数,再根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]代入计算即可.
解答 解:甲数的众数为7、8、6,甲数的中位数为7,甲数的平均数是:(7+8+6+8+6+5+9+10+7+4)÷10=7,
甲数的方差为:S甲2=$\frac{1}{10}$×[(7-7)2+(8-7)2+(6-7)2+(8-7)2+(6-7)2+(5-7)2+(9-7)2+(10-7)2+(7-7)2+(4-7)2]=3;
乙数的众数为7,乙数的中位数为7,乙数的平均数是:(9+5+7+8+7+6+8+6+7+7)÷10=7,
乙数的方差为:S乙2=$\frac{1}{10}$×[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]=1.5;
∵S乙2<S甲2,
∴乙样本情况较稳定.
点评 本题考查了众数,中位数,平均数,方差的定义,一般地设n个数据,x1,x2,…xn的平均数为$\frac{1}{n}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
5.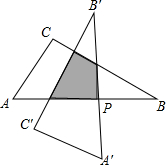 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )| A. | $\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{9}{4}$ | D. | $\frac{15}{4}$ |
2.某班主任老师为了对学生乱花钱的现象进行教育指导,对班里每位同学一周大约花钱数额进行了统计,如下表:
根据这个统计可知,该班学生一周花钱数额的众数、中位数是( )
| 花钱数额(元) | 5 | 10 | 15 | 20 | 25 |
| 学生人数 | 7 | 12 | 18 | 10 | 3 |
| A. | 15,15 | B. | 18,15 | C. | 25,18 | D. | 15,18 |
3.已知点M(-2,3)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
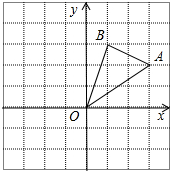 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1. 如图,将两块直角三角尺的直角顶点C叠放在一起,
如图,将两块直角三角尺的直角顶点C叠放在一起,