题目内容
13.从1,2,3,4这四个数中,随机抽取两个相加,和为偶数的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 列举出符合题意的各种情况的个数,再根据概率公式解答即可.
解答 解:画树形图得:
∴随机抽取两个相加,有12情况,和为偶数的有4种情况,
∴和为偶数的概率为$\frac{1}{3}$,
故选:D.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | 32-2a2=1 | B. | a6÷a3=a2 | C. | (a-b)2=a2-b2 | D. | 2a•4a=8a2 |
5.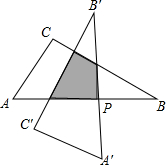 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )| A. | $\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{9}{4}$ | D. | $\frac{15}{4}$ |
2.某班主任老师为了对学生乱花钱的现象进行教育指导,对班里每位同学一周大约花钱数额进行了统计,如下表:
根据这个统计可知,该班学生一周花钱数额的众数、中位数是( )
| 花钱数额(元) | 5 | 10 | 15 | 20 | 25 |
| 学生人数 | 7 | 12 | 18 | 10 | 3 |
| A. | 15,15 | B. | 18,15 | C. | 25,18 | D. | 15,18 |
3.已知点M(-2,3)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
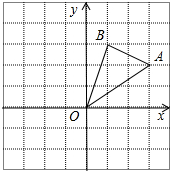 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.