题目内容
16.阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.例如:(x-1)2+3、(x-2)2+2x、($\frac{1}{2}$x-2)2+$\frac{3}{4}$x2是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出x2-4x+1三种不同形式的配方;
(2)将x4+x2y2+y4分解因式;
(3)已知a2+b2+c2=ab+3b+2c-4,求a+b+c的值.
分析 (1)直接利用完全平方公式结合已知变形得出答案;
(2)利用完全平方公式分解因式即可;
(3)首先将原式利用完全平方公式分解因式,进而得出答案.
解答 解:(1)x2-4x+1=(x-2)2-3,x2-4x+1=(x-1)2-2x,
x2-4x+1=(2x-1)2-3x2;
(2)x4+x2y2+y4
=x4+2x2y2+y4-x2y2,
=(x2+y2)2-x2y2,
=(x2+y2+xy)(x2+y2-xy);
(3)∵a2+b2+c2=ab+3b+2c-4,
∴(a-$\frac{1}{2}$b)2+$\frac{3}{4}$(b-2)2+(c-1)2=0,
故b=2,c=1,a=1,
则a+b+c=4.
点评 此题主要考查了因式分解的应用,正确应用乘法公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.当x为任意实数时,下列分式一定有意义的是( )
| A. | $\frac{x+1}{|x|}$ | B. | $\frac{x+1}{{x}^{2}}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x+1}{{x}^{2}-4}$ |
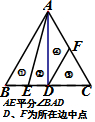
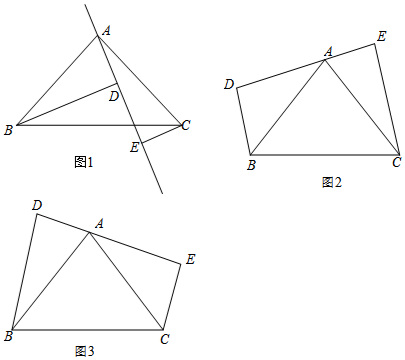
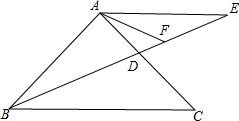 如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.