题目内容
4.在同一直角坐标系中,直线y=-x+3与y=3x-5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=-x+3与y=3x-5上的点.(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
分析 (1)分别令y=-x+3与y=3x-5中y=0求出x值,即可得出点A、B的坐标,联立两直线解析式成方程组,解方程组即可求出点C的坐标,再结合三角形的面积公式即可求出△ABC的面积;
(2)由点P在直线y=-x+3上,设点P(m,-m+3),由P、Q关于原点对称,由此可找出Q(-m,m-3),由点Q的坐标利用一次函数图象上点的坐标特征即可找出关于m的一元一次方程,解方程求出m值,将其代入点P的坐标中即可得出结论;
(3)由△QPC≌△ABC可得出CQ=CA,设点Q的坐标为(n,3n-5),由CQ=CA可得出$\sqrt{(n-2)^{2}+(3n-5-1)^{2}}$=$\sqrt{(3-2)^{2}+(0-1)^{2}}$,解之即可得出n的值,将其代入点Q的坐标即可得出结论.
解答 解:(1)依照题意画出图形,如图1所示.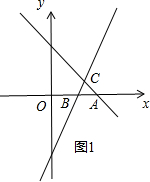
令y=-x+3中y=0,则x=3,
∴A(3,0);
令y=3x-5中y=0,则x=$\frac{5}{3}$,
∴B($\frac{5}{3}$,0);
联立两直线解析式成方程组,得:$\left\{\begin{array}{l}{y=-x+3}\\{y=3x-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴C(2,1).
S△ABC=$\frac{1}{2}$AB•yC=$\frac{1}{2}$(3-$\frac{5}{3}$)×1=$\frac{2}{3}$.
(2)∵点P在直线y=-x+3上,
∴设P(m,-m+3),
∵P、Q关于原点成中心对称,
∴Q(-m,m-3).
∵点Q在直线y=3x-5上,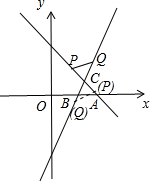
∴m-3=-3m-5,
解得:m=-$\frac{1}{2}$,
∴点P的坐标为(-$\frac{1}{2}$,$\frac{7}{2}$).
(3)依照题意画出图形,如图2所示.
∵△QPC≌△ABC,
∴CQ=CA.
设点Q的坐标为(n,3n-5),
则有$\sqrt{(n-2)^{2}+(3n-5-1)^{2}}$=$\sqrt{(3-2)^{2}+(0-1)^{2}}$,
解得:n=2+$\frac{\sqrt{5}}{5}$或n=2-$\frac{\sqrt{5}}{5}$,
∴点Q的坐标为(2+$\frac{\sqrt{5}}{5}$,1+$\frac{3\sqrt{5}}{5}$)或(2-$\frac{\sqrt{5}}{5}$,1-$\frac{3\sqrt{5}}{5}$).
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积公式、全等三角形的判定以及解一元一次方程,解题的关键是:(1)求出点A、B、C的坐标;(2)由一次函数图象上点的坐标特征找出关于m的一元一次方程;(3)由CQ=CA找出关于n的方程.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | 无实数根 | B. | 两个相等的实数根 | ||
| C. | 两个不相等的实数根 | D. | 不确定 |
| A. | $\left\{\begin{array}{l}{x+y=48}\\{3x=5y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=48}\\{5x=3y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=48}\\{x=2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=48}\\{y=2x}\end{array}\right.$ |
①角;②线段;③等腰三角形;④等边三角形;⑤三角形.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,△ABC为等边三角形,点P是边AC的延长线上一点,连接BP,作∠BPQ等于60°,直线PQ与直线BC交于点N.
如图,△ABC为等边三角形,点P是边AC的延长线上一点,连接BP,作∠BPQ等于60°,直线PQ与直线BC交于点N. 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.