题目内容
15．
如图，在△ABC中，∠B=50°，AE平分∠BAC，∠BAE=30°，则∠ACD=（ ）| A． | 100° | B． | 120° | C． | 135° | D． | 110° |
分析 由角平分线的定义可求得∠BAC，再利用外角的性质可求得∠ACD．
解答 解：
∵AE平分∠BAC，
∴∠BAC=2∠BAE=2×30°=60°，
∵∠ACD是△ACD的外角，
∴∠ACD=∠B+∠BAC=50°+60°=110°，
故选D．
点评 本题主要考查三角形外角的性质，掌握三角形的外角等于不相邻两内角的和是解题的关键．
练习册系列答案
步步高达标卷系列答案
相关题目
5．
如图，在△ABC中，∠B=60°，∠C=90°，AC=2，则AB=（ ）
如图，在△ABC中，∠B=60°，∠C=90°，AC=2，则AB=（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |
6．甲、乙、丙、丁四人商量周末出游．甲说：“乙去，我就肯定去．”乙说：“丙去我就不去．”丙说：“无论丁去不去，我都去．”丁说：“甲乙中至少有一人去，我就去．”以下结论可能正确的是（ ）
| A． | 甲一个人去了 | B． | 乙、丙两个人去了 | ||
| C． | 甲、丙、丁三个人去了 | D． | 四个人都去了 |
3．
如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=118°，则∠A的度数为（ ）
如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=118°，则∠A的度数为（ ）| A． | 65° | B． | 66° | C． | 70° | D． | 78° |
10．
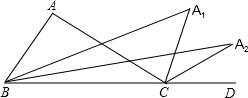如图，△ABC中，∠A=α°，延长BC到D，∠ABC与∠ACD的平分线相交于点A1，∠A1BC与∠A1CD的平分线相交于点A2，依此类推，∠An-1BC与∠An-1CD的平分线相交于点An，则∠An的度数为（ ）
如图，△ABC中，∠A=α°，延长BC到D，∠ABC与∠ACD的平分线相交于点A1，∠A1BC与∠A1CD的平分线相交于点A2，依此类推，∠An-1BC与∠An-1CD的平分线相交于点An，则∠An的度数为（ ）| A． | ${（{\frac{α}{n}}）°}$ | B． | ${（{\frac{α}{2n}}）°}$ | C． | ${（{\frac{α}{2^n}}）°}$ | D． | ${（{\frac{α}{{{2^{n+1}}}}}）°}$ |
如图，正方形ABCD中，点E、F分别为AB、CD上的点，且AE=CF=$\frac{1}{3}$AB，点O为线段EF的中点，过点O作直线与正方形的一组对边分别交于P、Q两点，并且满足PQ=EF，则这样的直线PQ（不同于EF）有3条．
7．
如图，在△ABC中，∠ACB=90°，CD为∠ACB的平分线，过点D作DE⊥BC于E，DF⊥AC于F，若AF=8，BE=6，则CE的长为（ ）
如图，在△ABC中，∠ACB=90°，CD为∠ACB的平分线，过点D作DE⊥BC于E，DF⊥AC于F，若AF=8，BE=6，则CE的长为（ ）| A． | 8 | B． | $4\sqrt{3}$ | C． | 7 | D． | 6 |
4．如果-x×（-4）=$\frac{8}{5}$，则x的值为（ ）
| A． | $\frac{2}{5}$ | B． | -$\frac{2}{5}$ | C． | $\frac{5}{2}$ | D． | -$\frac{5}{2}$ |
8．
如图，在⊙O中，AB为直径，点C在⊙O上，连接AC，BC，D是劣弧AC的中点，连接OD，交AC于点E，连接BD，交CE于点F，若EF：CF=1：3，OE=1.5，则BD的长度为（ ）
如图，在⊙O中，AB为直径，点C在⊙O上，连接AC，BC，D是劣弧AC的中点，连接OD，交AC于点E，连接BD，交CE于点F，若EF：CF=1：3，OE=1.5，则BD的长度为（ ）| A． | 3 | B． | 5 | C． | 2$\sqrt{3}$ | D． | 2$\sqrt{5}$ |