题目内容
20. 如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=$\frac{1}{3}$AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有3条.
如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=$\frac{1}{3}$AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有3条.
分析 能画3条:①与EF互相垂直且垂足为O,构建直角三角形,可以证明两直角三角形全等得EF=PQ;
②在AD上截取AP=$\frac{1}{3}$AD,连接PO延长得到PQ;
③同理在AB了截取BQ=$\frac{1}{3}$AB,连接QO并延长得到PQ.
解答 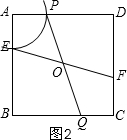
 解:这样的直线PQ(不同于EF)有3条,
解:这样的直线PQ(不同于EF)有3条,
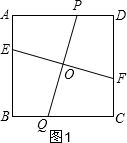
①如图1,过O作PQ⊥EF,交AD于P,BC于Q,
则PQ=EF;
②如图2,以点A为圆心,以AE为半径画弧,交AD于P,连接PO并延长交BC于Q,则PQ=EF;
③如图3,以B为圆心,以AE为半径画弧,交AB于Q,连接QO并延长交DC于点P,则PQ=EF.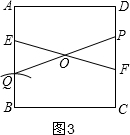
点评 本题考查了正方形的性质和全等三角形的性质与判定,本题虽然是做一条线段与EF相等,实际上是做好两件事:①画线段PQ,②能证明这两条线段相等,这比证明更为复杂,因此首先要构建直角三角形全等,找到与EF相等的边长的位置,本题的线段不止一条,容易丢解,要思考周全.

练习册系列答案
相关题目
10. 如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
 如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 无法确定 |
11.已知x+y=6,x-y=1,则x2-y2等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
8.有下面4个数:8、5、11、x,它们的最大值与最小值的差为10,则x的值为( )
| A. | 6 | B. | 1 | C. | 15 | D. | 1或15 |
15. 如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )
如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )
 如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )
如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )| A. | 100° | B. | 120° | C. | 135° | D. | 110° |
12.身份证号码告诉我们很多信息,某人得身份证号码是610323196209232913,其中,61、03、23是此人所属的省(市、自治区)、市、县(市、区)的编码,1962、09、23是此人出生的年、月、日,291是顺序码,3为校验码.那么身份证号码是321084198101208022的人的生日是( )
| A. | 8月10日 | B. | 10月12日 | C. | 1月20日 | D. | D、12月8日 |
13. 如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )
如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )
 如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )
如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{12}$ | D. | $\frac{3}{4}$ |