题目内容
15．
已知二次函数y=x2-2x+m的部分图象如图所示，则关于x的一元二次方程x2-2x+m=0的解为x1=-1，x2=3．
分析 求得抛物线与x轴的交点坐标，交点的横坐标就是方程的解．
解答 解：（3，0）关于x=1的对称点是（-1，0）．
则一元二次方程x2-2x+m=0的解为x1=-1，x2=3．
故答案是：x1=-1，x2=3．
点评 本题考查了抛物线与x轴的交点，与x轴交点的横坐标就是令y=0所得方程的解．
练习册系列答案
全能测控一本好卷系列答案
相关题目
18．如果是$\root{3}{x-6}$的6-x立方根，那么x的值（ ）
| A． | 0 | B． | 3 | C． | 5 | D． | 6 |
将一副三角板中的两块直角三角尺按如图方式叠放在一起（其中∠ACB=∠E=90°，∠A=60°，∠B=30°，∠ECD=∠EDC=45°）．
7．已知△ABC∽△A′B′C′，AD、A′D′分别是△ABC和△A′B′C′的对应高，且AD：A′D′=2：3，则下列结论正确的是（ ）
| A． | AB：A′B′=2：3 | B． | S△ABC：S△A′B′C′=2：3 | ||
| C． | （AB+BC+AC）：（A′B′+B′C′+A′C′）=4：9 | D． | （AD+BC）：（A′D′+B′C′）=4：9 |
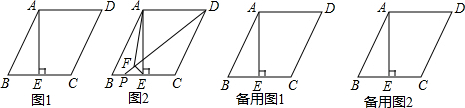
在如图所示的方格中分别填入-8，-6，-4，-2，2，4，6，8这8个数，使得每行的三个数，每列的三个数，斜对角的三个数之和都相等．